题目内容
3. 矩形ABCD中,M是AD的中点,N是BC的中点,点P是CD的延长线连接PM延长交AC于点Q,连接PN,QN.
矩形ABCD中,M是AD的中点,N是BC的中点,点P是CD的延长线连接PM延长交AC于点Q,连接PN,QN.求证:∠QNM=∠PNM.
分析 先延长QN,交DC的延长线于点E,根据矩形ABCD中,M是AD的中点,N是BC的中点,得出MN||PE,再根据平行线分线段成比例定理,得出ON:CE=QO:QC=OM:CP,再根据全等三角形的性质,得出MO=NO,及CP=CE,最后根据∠QNM=∠QEC,∠PNM=∠NPC,∠NPC=∠NEC,运用等量代换可以得出结论.
解答  证明:延长QN,交DC的延长线于点E,
证明:延长QN,交DC的延长线于点E,
∵矩形ABCD中,M是AD的中点,N是BC的中点,
∴DM=CN,DM∥CN,
∴平行四边形CDMN中,MN||PE,
∴∠QNM=∠QEC,∠PNM=∠NPC,且ON:CE=QO:QC=OM:CP,
又∵∠AOM=∠CON,∠OAM=∠OCN,AM=CN,
∴△AOM≌△CON,
∴MO=NO,
∴CP=CE,
∴NC垂直平分PE,
∴NP=NE,
∴∠NPC=∠NEC,
∴∠QNM=∠PNM.
点评 本题主要考查了矩形的性质、全等三角形的判定与性质,以及平行线分线段成比例定理的综合应用,解决问题的关键是作辅助线构造同位角.解题时注意:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.

练习册系列答案
相关题目
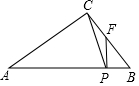 如图,在△ABC中,∠ACB=90°,BC=6,AC=8,点P为边AB上的一个动点,过点P作AB的垂线交BC所在的直线于点F,连接CP,当△CFP为等腰三角形时,求PF的长.
如图,在△ABC中,∠ACB=90°,BC=6,AC=8,点P为边AB上的一个动点,过点P作AB的垂线交BC所在的直线于点F,连接CP,当△CFP为等腰三角形时,求PF的长.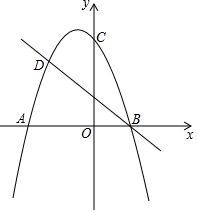 如图所示,在直角坐标平面中,二次函数y=-x2+kx+4的图象与y轴交于C点,与x轴交于点A(-3,0)和B点,一次函数y=-x+b图象经过点B交抛物线于另一点D.
如图所示,在直角坐标平面中,二次函数y=-x2+kx+4的图象与y轴交于C点,与x轴交于点A(-3,0)和B点,一次函数y=-x+b图象经过点B交抛物线于另一点D.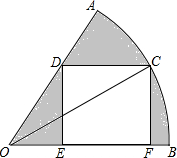 如图,在扇形AOB中,∠AOB=60°,A0O=6,OC平分∠AOB,交$\widehat{AB}$于C,CF⊥OB于F,CD∥OB,交OA于D,DE⊥OB于E.求图中阴影部分的面积.
如图,在扇形AOB中,∠AOB=60°,A0O=6,OC平分∠AOB,交$\widehat{AB}$于C,CF⊥OB于F,CD∥OB,交OA于D,DE⊥OB于E.求图中阴影部分的面积.