题目内容
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
分析：先根据表中x=0时，y=1；x=-1时，y=-3；x=1时，y=3代入二次函数y=ax2+bx+c的解析式，再根据二次函数的性质对各小题进行逐一分析．
解答：解：∵x=0时，y=1；x=-1时，y=-3；x=1时，y=3代入二次函数y=ax2+bx+c的解析式得，
，解得
，
∴此二次函数的解析式为：y=-x2+3x+1，
∵a=-1＜0，
∴此抛物线开口向下，故①错误；
∵c=1＞0，
∴抛物线与y轴交于正半轴，故②错误；
∵当x=4时，y=-42+3×4+1=-3＜0，故③错误；
令-x2+3x+1=0，则x=
，
∴方程的正根为x=
=
，
∵3＜
＜4，
∴3+3＜3+
＜3+4，
∴3＜
＜3.5，
∴方程ax2+bx+c=0的正根在3与4之间，故④正确．
故答案为④．
|
|
∴此二次函数的解析式为：y=-x2+3x+1，
∵a=-1＜0，
∴此抛物线开口向下，故①错误；
∵c=1＞0，
∴抛物线与y轴交于正半轴，故②错误；
∵当x=4时，y=-42+3×4+1=-3＜0，故③错误；
令-x2+3x+1=0，则x=
-3±
| ||
| -2 |
∴方程的正根为x=
-3-
| ||
| -2 |
3+
| ||
| 2 |
∵3＜
| 13 |
∴3+3＜3+
| 13 |
∴3＜
3+
| ||
| 2 |
∴方程ax2+bx+c=0的正根在3与4之间，故④正确．
故答案为④．
点评：本题考查的是抛物线与x轴的交点，能根据题意得出抛物线的解析式是解答此题的关键．
练习册系列答案
相关题目
-2
的负倒数是（ ）
| 1 |
| 2 |
A、-2
| ||
B、2
| ||
C、-
| ||
D、
|
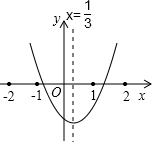小明从图表示的二次函数y=ax2+bx+c的图象中，观察得出了下面五条信息：
等的9块长方形（如图所示），种上各种花卉，经市场预测，绿化每平方米造价100元．