题目内容
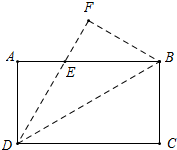 把一张长方形的纸ABCD沿对角线BD翻折,使得C点落在点F处,DF交AB于E,已知AE=2,DC=6,求∠ADE.
把一张长方形的纸ABCD沿对角线BD翻折,使得C点落在点F处,DF交AB于E,已知AE=2,DC=6,求∠ADE.考点:翻折变换(折叠问题)
专题:
分析:首先求出线段DE、AE的长度,然后利用直角三角形的边角关系即可求出∠ADE的大小.
解答: 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴AB∥DC,AB=CD=6;而AE=2,
∴∠EBD=∠BDC,BE=6-2=4;
由题意得:∠EDB=∠BDC,
∴∠EBD=∠EDB,
∴DE=BE=4;
在直角△ADE中:
∵sin∠ADE=
=
=
,
∴∠ADE=30°.
 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,∴AB∥DC,AB=CD=6;而AE=2,
∴∠EBD=∠BDC,BE=6-2=4;
由题意得:∠EDB=∠BDC,
∴∠EBD=∠EDB,
∴DE=BE=4;
在直角△ADE中:
∵sin∠ADE=
| AE |
| DE |
| 2 |
| 4 |
| 1 |
| 2 |
∴∠ADE=30°.
点评:该命题主要考查了翻折变换的性质及其应用问题;解题的关键是根据题意证明DE=BE=4,然后利用直角△ADE的边角关系来分析、判断、求解.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
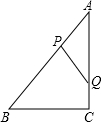 如图,Rt△ABC中,∠C=90°,AB=10,cosA=
如图,Rt△ABC中,∠C=90°,AB=10,cosA= 如图,AB是⊙O1的直径,AO1是⊙O2的直径,弦MN∥AB,且MN与⊙O2相切于点C,若⊙O1的半径为2.阴影部分的面积=
如图,AB是⊙O1的直径,AO1是⊙O2的直径,弦MN∥AB,且MN与⊙O2相切于点C,若⊙O1的半径为2.阴影部分的面积=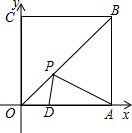 正方形OABC位于坐标系如图 边长为8,在OA上有一点D坐标(6,0).在对角线OB上有一动点P,使PA+PD最短,则最短距离为
正方形OABC位于坐标系如图 边长为8,在OA上有一点D坐标(6,0).在对角线OB上有一动点P,使PA+PD最短,则最短距离为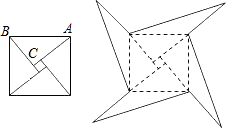 如图,左图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若两直角边AC=6,BC=4,现将四个直角三角形中边长为4的直角边分别向外延长一倍,延长后得到右图所示的“数学风车”,则该“数学风”所围成的总面积是
如图,左图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若两直角边AC=6,BC=4,现将四个直角三角形中边长为4的直角边分别向外延长一倍,延长后得到右图所示的“数学风车”,则该“数学风”所围成的总面积是