题目内容
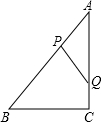 如图,Rt△ABC中,∠C=90°,AB=10,cosA=
如图,Rt△ABC中,∠C=90°,AB=10,cosA=| 4 |
| 5 |
(1)当△APQ和△ABC相似时,求AP的长;
(2)联结PC、BQ,如果BQ⊥PC,求AP的长.
考点:相似三角形的判定与性质
专题:
分析:(1)分2种情况讨论①PQ∥BC时,②PQ不平行于BC时,分别证明即可;
(2)过P作PE⊥AC于E,可证△BCQ∽△PCE,即可求得AP的值,即可解题.
(2)过P作PE⊥AC于E,可证△BCQ∽△PCE,即可求得AP的值,即可解题.
解答:解:(1)∵Rt△ABC中,cosA=
,AB=10,
∴BC=6,AC=8,
①当PQ∥BC时,当AP:CQ=5:4,AP:CQ=5:4,
∴P、Q分别为AB,AC中点;AP=5,
②当PQ不平行于BC,△APQ∽△ABC时,
=
,
=
,
∵AP:CQ=5:4,
∴AQ:CQ=25:16,
此时PA=8
,
∴当AP=5或8
时,△APQ∽△ABC.
(2)过P作PE⊥AC于E.

∵BQ⊥PC∠C=90°,
∴∠CBQ=∠PCE,
∵∠BCQ=∠CEP=90°,
∴△BCQ∽△PCE,
∴PE:CQ=CE:BC,
∵AP=5x AE=PA×cosA=4x∴PE=3x,
CE=AC-AE=8-4x,
∴3x:4x=(8-4x):6,
∴x=
AP=5×
=
.
| 4 |
| 5 |
∴BC=6,AC=8,
①当PQ∥BC时,当AP:CQ=5:4,AP:CQ=5:4,
∴P、Q分别为AB,AC中点;AP=5,
②当PQ不平行于BC,△APQ∽△ABC时,
| AP |
| AC |
| AQ |
| AB |
| AP |
| AQ |
| 4 |
| 5 |
∵AP:CQ=5:4,
∴AQ:CQ=25:16,
此时PA=8
| 20 |
| 41 |
∴当AP=5或8
| 20 |
| 41 |
(2)过P作PE⊥AC于E.

∵BQ⊥PC∠C=90°,
∴∠CBQ=∠PCE,
∵∠BCQ=∠CEP=90°,
∴△BCQ∽△PCE,
∴PE:CQ=CE:BC,
∵AP=5x AE=PA×cosA=4x∴PE=3x,
CE=AC-AE=8-4x,
∴3x:4x=(8-4x):6,
∴x=
| 7 |
| 8 |
| 7 |
| 8 |
| 35 |
| 8 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 如图,已知:△ABC内接于圆O,点D在OC的延长线上,若∠B=∠D=30°
如图,已知:△ABC内接于圆O,点D在OC的延长线上,若∠B=∠D=30°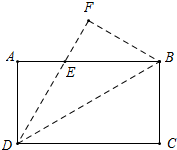 把一张长方形的纸ABCD沿对角线BD翻折,使得C点落在点F处,DF交AB于E,已知AE=2,DC=6,求∠ADE.
把一张长方形的纸ABCD沿对角线BD翻折,使得C点落在点F处,DF交AB于E,已知AE=2,DC=6,求∠ADE.