题目内容
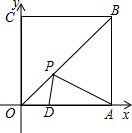正方形OABC位于坐标系如图 边长为8，在OA上有一点D坐标（6，0）．在对角线OB上有一动点P，使PA+PD最短，则最短距离为考点：轴对称-最短路线问题,坐标与图形性质
专题：
分析：连接CD，根据四边形OABC是正方形可知A、C关于直线OB对称，故CD的长即为PA+PD的最短长度，根据勾股定理求出CD的长即可．
解答：
解：连接CD，
∵四边形OABC是正方形，
∴A、C关于直线OB对称，
∴CD的长即为PA+PD的最短长度，
∵点D坐标（6，0）．
∴OD=6，
∴CD=
=
=10．
故答案为：10．
解：连接CD，∵四边形OABC是正方形，
∴A、C关于直线OB对称，
∴CD的长即为PA+PD的最短长度，
∵点D坐标（6，0）．
∴OD=6，
∴CD=
| OC2+OD2 |
| 82+62 |
故答案为：10．
点评：本题考查的是轴对称-最短路线问题，熟知两点之间，线段最短是解答此题的关键．
练习册系列答案
相关题目
如图，已知：△ABC内接于圆O，点D在OC的延长线上，若∠B=∠D=30°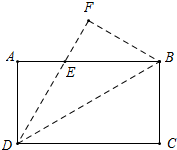
把一张长方形的纸ABCD沿对角线BD翻折，使得C点落在点F处，DF交AB于E，已知AE=2，DC=6，求∠ADE．
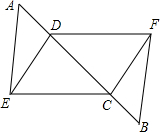已知，如图，点A、D、C、B在同一条直线上，AD=BC，AE=BF，CE=DF．求证：
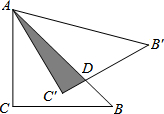如图，△ABC为等腰直角三角形，AC=CB，∠ACB=90°，将△ABC绕点A逆时针旋转后得到△AB′C′，若AC=6cm，△AB′C′与△ABC重叠部分面积为6
在数轴上表示下列各数，并用“＜”连接起来．-3.5，-（-2），（-2）2，