题目内容
17.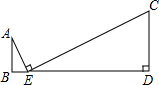 如图,AB⊥BD,垂足为B,CD⊥BD,垂足为D,AE⊥CE,垂足为E,且点B、E、D在同一条直线上,已知BE=5,AB=6,ED=12,求CD的长.
如图,AB⊥BD,垂足为B,CD⊥BD,垂足为D,AE⊥CE,垂足为E,且点B、E、D在同一条直线上,已知BE=5,AB=6,ED=12,求CD的长.
分析 由AB⊥BD,CD⊥BD,AE⊥CE,推出∠B=∠AEB=∠D,由于∠A+∠AEB=90°,∠AEB+∠CED=90°,得到∠A=∠CED,于是有△ABE∽△EDC,根据相似三角形的性质即可得到结论.
解答 解:∵AB⊥BD,CD⊥BD,AE⊥CE,
∴∠B=∠AEB=∠D=90°,
∴∠A+∠AEB=90°,∠AEB+∠CED=90°,
∴∠A=∠CED,
∴△ABE∽△EDC,
∴$\frac{AB}{ED}=\frac{BE}{CD}$,
∵AB=6,ED=12,BE=5,
∴CD=10.
点评 本题主要考查了相似三角形的判定和性质,熟记相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
7. 两个有理数a,b在数轴上位置如图,下列四个式子中运算结果为正数的式子是( )
两个有理数a,b在数轴上位置如图,下列四个式子中运算结果为正数的式子是( )
 两个有理数a,b在数轴上位置如图,下列四个式子中运算结果为正数的式子是( )
两个有理数a,b在数轴上位置如图,下列四个式子中运算结果为正数的式子是( )| A. | $\frac{a}{b}$ | B. | b-a | C. | ab | D. | a+b |
5.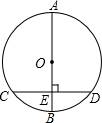 如图,AB为⊙O的直径,弦CD垂直平分半径OB,垂足为E,CD=6cm,则直径AB的长是( )
如图,AB为⊙O的直径,弦CD垂直平分半径OB,垂足为E,CD=6cm,则直径AB的长是( )
 如图,AB为⊙O的直径,弦CD垂直平分半径OB,垂足为E,CD=6cm,则直径AB的长是( )
如图,AB为⊙O的直径,弦CD垂直平分半径OB,垂足为E,CD=6cm,则直径AB的长是( )| A. | 10cm | B. | 3$\sqrt{2}$cm | C. | 4$\sqrt{2}$cm | D. | 4$\sqrt{3}$cm |
9.计算:1002-2×100×99+992=( )
| A. | 0 | B. | 1 | C. | -1 | D. | 39601 |
6.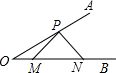 如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )
如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )
 如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )
如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )| A. | 8 | B. | 6 | C. | 2$\sqrt{3}$+4 | D. | 2$\sqrt{3}$+2 |
7.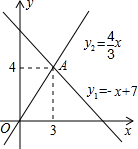 如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
 如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )| A. | x>3 | B. | x<3 | C. | x>4 | D. | x<4 |
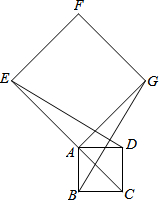 如图,在正方形ABCD中,延长对角线CA到点E,以AE为边作正方形AEFG,连接BG、DE.
如图,在正方形ABCD中,延长对角线CA到点E,以AE为边作正方形AEFG,连接BG、DE.