题目内容
12.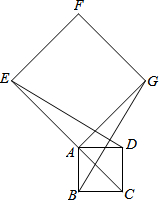 如图,在正方形ABCD中,延长对角线CA到点E,以AE为边作正方形AEFG,连接BG、DE.
如图,在正方形ABCD中,延长对角线CA到点E,以AE为边作正方形AEFG,连接BG、DE.(1)求证:△ABG≌△ADE;
(2)当AB=$\sqrt{2}$,AG=3时,求线段BG的长度.
分析 (1)由四边形ABCD是正方形,得到AB=AD,∠BAD=90°,根据四边形AEFG是正方形,得到AE=AG,∠EAG=90°,于是得到∠BAD=∠EAG,证得∠BAG=∠DAE,于是得到结论;
(2)如图,连接BD交AC于点H,根据四边形ABCD是正方形,于是得到AH=DH,∠AHD=90°,由于$AD=AB=\sqrt{2}$,求出AH=DH=1,在Rt△EHD中,由勾股定理得:$ED=\sqrt{E{H^2}+D{H^2}}=\sqrt{17}$,又由(1)△ABG≌△ADE得到BG=ED,于是结论可得.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵四边形AEFG是正方形,
∴AE=AG,∠EAG=90°,
∴∠BAD=∠EAG,
∴∠BAD+∠DAG=∠EAG+∠DAG,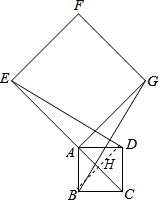
∴∠BAG=∠DAE,
在△ABG与△ADE中,
$\left\{\begin{array}{l}{AG=AE}\\{∠BAG=∠DAE}\\{AB=AD}\end{array}\right.$,
∴△ABG≌△ADE(SAS);
(2)解:如图,连接BD交AC于点H,
∵四边形ABCD是正方形,
∴AH=DH,∠AHD=90°,
又∵$AD=AB=\sqrt{2}$,
∴AH=DH=1,
又∵四边形AEFG是正方形,
∴AE=AG=3,
∴EH=AE+AH=4,
在Rt△EHD中,由勾股定理,得:$ED=\sqrt{E{H^2}+D{H^2}}=\sqrt{17}$,
又由(1)△ABG≌△ADE,
∴BG=ED,
∴$BG=\sqrt{17}$.
点评 本题考查了全等三角形的判定和性质,正方形的性质,勾股定理,证得△ABG≌△ADE是解题的关键.

练习册系列答案
相关题目
 一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,若BC=10,CD=5$\sqrt{3}$-5.(结果保留根号)
一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,若BC=10,CD=5$\sqrt{3}$-5.(结果保留根号)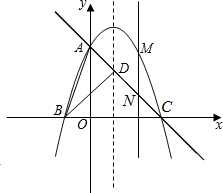 如图,已知抛物线y=ax2+bx=3与y轴交于点A,与x轴交于点B(-1,0)和点C(3,0).
如图,已知抛物线y=ax2+bx=3与y轴交于点A,与x轴交于点B(-1,0)和点C(3,0). 已知,如图,?ABCD中,AE平分∠BAD,交BC于点E,CF平分∠DCB,交AD于点F.求证:△ABE≌△CDF.
已知,如图,?ABCD中,AE平分∠BAD,交BC于点E,CF平分∠DCB,交AD于点F.求证:△ABE≌△CDF.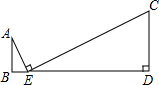 如图,AB⊥BD,垂足为B,CD⊥BD,垂足为D,AE⊥CE,垂足为E,且点B、E、D在同一条直线上,已知BE=5,AB=6,ED=12,求CD的长.
如图,AB⊥BD,垂足为B,CD⊥BD,垂足为D,AE⊥CE,垂足为E,且点B、E、D在同一条直线上,已知BE=5,AB=6,ED=12,求CD的长.