题目内容
7.从-1,0,1,2这4个数中,随机抽取一个数记为a,放回并混在一起,再随机抽取一个数记为b,则使得关于x的一次函数y=ax+b不经过第一象限的概率为$\frac{1}{8}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与使得关于x的一次函数y=ax+b不经过第一象限的情况,再利用概率公式求解即可求得答案.
解答 解:画树状图得:
∵共有16种等可能的结果,使得关于x的一次函数y=ax+b不经过第一象限的有2种情况,
∴使得关于x的一次函数y=ax+b不经过第一象限的概率为:$\frac{2}{16}$=$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 此题考查了列表法或树状图法求概率以及一次函数的性质.注意掌握一次函数y=ax+b不经过第一象限的特点是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.化简$\frac{3}{\sqrt{6}}$的结果是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$$\sqrt{6}$ | D. | 以上答案都不对 |
15.下列图形中,既是轴对称又是中心对称的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列各命题的逆命题成立的是( )
| A. | 对顶角相等 | B. | 如果a=b,那么|a|=|b| | ||
| C. | 全等三角形的对应角相等 | D. | 两直线平行,同位角相等 |
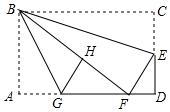 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论: 如图,在⊙O中,OB为半径,AB是⊙O的切线,OA与⊙O相交于点C,∠A=30°,OA=8,则阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}$π.
如图,在⊙O中,OB为半径,AB是⊙O的切线,OA与⊙O相交于点C,∠A=30°,OA=8,则阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}$π.