题目内容
4.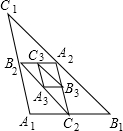 如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…;以此类推,则△A4B4C4的周长是2,△AnBnCn的周长是$\frac{{2}^{5}}{{2}^{n-1}}$.
如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…;以此类推,则△A4B4C4的周长是2,△AnBnCn的周长是$\frac{{2}^{5}}{{2}^{n-1}}$.
分析 由三角形的中位线定理得:B2C2,A2C2,A2B2分别等于A1B1、B1C1、C1A1的$\frac{1}{2}$,所以△A2B2C2的周长等于△A1B1C1的周长的一半,以此类推可求出结论.
解答 解:∵△A1B1C1中,A1B1=4,A1C1=5,B1C1=7,
∴△A1B1C1的周长是16,
∵A2,B2,C2分别是边B1C1,A1C1,A1B1的中点,
∴B2C2,A2C2,A2B2分别等于A1B1、B1C1、C1A1的$\frac{1}{2}$,
…,
以此类推,则△A4B4C4的周长是$\frac{1}{{2}^{3}}$×16=2;
∴△AnBnCn的周长是$\frac{{2}^{5}}{2n-1}$,
故答案为:2,$\frac{{2}^{5}}{{2}^{n-1}}$.
点评 本题考查了三角形的中位线定理,中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若关于x的不等式组$\left\{\begin{array}{l}{\frac{x+15}{2}>x-3}\\{\frac{2x+2}{3}<x+a}\end{array}\right.$的解只有4个整数解,则a的取值范围是( )
| A. | -$\frac{14}{3}$<a<-5 | B. | -5≤a<-$\frac{14}{3}$ | C. | -5<a≤-$\frac{14}{3}$ | D. | -$\frac{14}{3}$<a≤-5 |
14.新泰市2014级四年制学生人数约为1.33万名,从中抽取300名学生的八年级上学期其中考试数学成绩进行分析,在本次调查中,样本指的是( )
| A. | 300名考生的数学成绩 | B. | 300 | ||
| C. | 1.33万名考生的数学成绩 | D. | 300名考生 |
 如图,已知?ABCD中,对角线AC与BD交于点O,∠ABD=2∠DBC,AE⊥BD于E.
如图,已知?ABCD中,对角线AC与BD交于点O,∠ABD=2∠DBC,AE⊥BD于E.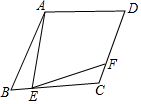 如图,四边形ABCD是菱形.∠ABC=60°,点E是BC边上一点,∠AEF=60°,且EF交直线CD于点F,求证:AE=EF.
如图,四边形ABCD是菱形.∠ABC=60°,点E是BC边上一点,∠AEF=60°,且EF交直线CD于点F,求证:AE=EF.