题目内容
11.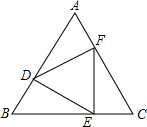 如图,在等边三角形ABC的三边上,分别取点D,E,F,使得△DEF为等边三角形,求证:AD=BE=CF.
如图,在等边三角形ABC的三边上,分别取点D,E,F,使得△DEF为等边三角形,求证:AD=BE=CF.
分析 只要证明△ADF≌△BED,得AD=BE,同理可证:BE=CF,由此即可证明.
解答 解:在等边三角形ABC中,∠A=∠B=60°.
∴∠AFD+∠ADF=120°.
∵△DEF为等边三角形,
∴∠FDE=60°,DF=ED.
∵∠BDE+∠EDF+∠ADF=180°,
∴∠BDE+∠ADF=120°.
∴∠BDE=∠AFD.
在△ADF和△BED中,
$\left\{\begin{array}{l}{∠A=∠B}\\{∠AFD=∠BDE}\\{DF=ED}\end{array}\right.$,
∴△ADF≌△BED.
∴AD=BE,同理可证:BE=CF.
∴AD=BE=CF.
点评 本题考查等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
1.一个事件的概率不可能是( )
| A. | $\frac{3}{2}$ | B. | 0 | C. | 1 | D. | $\frac{1}{3}$ |
16.下列大学的校徽图案是轴对称图形的是( )
| A. |  清华大学 | B. |  北京大学 | C. |  人民大学 | D. |  浙江大学 |
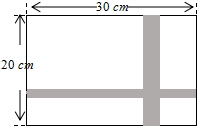 如图,要设计一副宽20cm、长30cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?
如图,要设计一副宽20cm、长30cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm? 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).