题目内容
18．当k=12时，双曲线y=$\frac{k}{x}$当过点（$\sqrt{3}$，4$\sqrt{3}$）．分析 直接把点（$\sqrt{3}$，4$\sqrt{3}$）代入双曲线y=$\frac{k}{x}$，求出k的值即可．
解答 解：∵双曲线y=$\frac{k}{x}$当过点（$\sqrt{3}$，4$\sqrt{3}$），
∴k=$\sqrt{3}$×4$\sqrt{3}$=12．
故答案为：12．
点评 本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
相关题目
请你在数轴上画出表示$\sqrt{2}$的点（保留作图痕迹）
13．使式子$\frac{x+3}{x-3}$÷$\frac{x+5}{x-4}$有意义的x值是（ ）
| A． | x≠3，且x≠-5 | B． | x≠3，且x≠4 | C． | x≠4且 x≠-5 | D． | x≠3，且x≠4且x≠-5 |
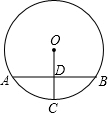如图，AB是⊙O的弦，半径OC⊥AB于点D，且AB=8cm，OC=5cm，求DC的长．