题目内容
若一个三角形的三边长a，b，c满足a2-2ab+b2+ac-bc=0，则这个三角形是（ ）
| A、直角三角形 |
| B、等边三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
考点：因式分解的应用
专题：
分析：首先把式子a2-2ab+b2+ac-bc=0分组分解因式，进一步探讨得出三边关系即可判定．
解答：解：∵a2-2ab+b2+ac-bc=0，
∴（a-b）（a-b+c）=0，
∵a，b，c为三角形的三边长，
∴a-b=0，a-b+c＞0，
∴a=b，
∴这个三角形是等腰三角形．
故选：C．
∴（a-b）（a-b+c）=0，
∵a，b，c为三角形的三边长，
∴a-b=0，a-b+c＞0，
∴a=b，
∴这个三角形是等腰三角形．
故选：C．
点评：此题考查因式分解的运用，注意分组分解，掌握三角形三边关系解决问题．
练习册系列答案
相关题目
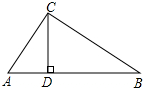如图，△ABC中，∠ACB=90°，CD是高，若AB=13cm，AC=5cm，求CD的长．