题目内容
14.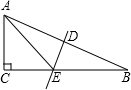 在△ABC中,DE垂直平分斜边AB,分别交AB、BC于D、E.
在△ABC中,DE垂直平分斜边AB,分别交AB、BC于D、E.(1)若∠CAE=∠B+30°,求∠B的度数;
(2)若∠B=15°,AC=a,AB=b,求DE长(用含a、b的代数式表示)
分析 (1)由DE垂直平分斜边AB,得到AE=BE,根据等腰三角形的性质得到AE=BE,求得∠EAD=∠B,由外角的性质得到∠AEC=∠B+∠BAE=2∠B,列方程即可得到结论;
(2)由(1)知∠AEC=2∠B,根据外角的性质得到∠AEC=30°,根据直角三角形的性质得到AE=2a,根据勾股定理即可得到结论.
解答 解:(1)∵DE垂直平分斜边AB,
∴AE=BE,
∴∠EAD=∠B,
∵∠C=90°,
∴∠CAE+∠AEC=90°,
∵∠AEC=∠B+∠BAE=2∠B,
∴∠B+30°+2∠B=90°,
解得:∠B=20°;
(2)由(1)知∠AEC=2∠B,
∵∠B=15°,
∴∠AEC=30°,
∵AC=a,
∴AE=2a,
∵AD=$\frac{1}{2}$AB=$\frac{1}{2}$b,
∴DE=$\sqrt{A{E}^{2}-A{D}^{2}}$=$\frac{1}{2}$$\sqrt{16{a}^{2}-{b}^{2}}$.
点评 本题主要考查线段垂直平分线的性质,利用直角三角形的两锐角互余得到关于∠B的方程求得∠B是解题的关键.

练习册系列答案
相关题目
6.下列式子中是分式的是( )
| A. | -3x | B. | -$\frac{a}{3π}$ | C. | $\frac{3}{5+y}$ | D. | $\frac{2}{3}$x2y |
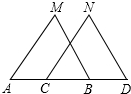 如图,A、C、B、D在同一条直线上,MB=ND,MB∥ND,要使△ABM≌△CDN,还需要添加一个条件为:∠M=∠N或∠A=∠NCD或AM∥CN或AB=CD.
如图,A、C、B、D在同一条直线上,MB=ND,MB∥ND,要使△ABM≌△CDN,还需要添加一个条件为:∠M=∠N或∠A=∠NCD或AM∥CN或AB=CD.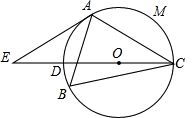 已知:△ABC内接于⊙O,∠B=60°,点E是直径CD的延长线上的一点,且AE=AC.
已知:△ABC内接于⊙O,∠B=60°,点E是直径CD的延长线上的一点,且AE=AC.