题目内容
17.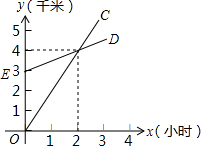 如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们的距离s(千米)与所用的时间t(小时)之间的函数关系分别如图中的射线OC和ED,当他们行走4小时后,他们之间的距离为3千米.
如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们的距离s(千米)与所用的时间t(小时)之间的函数关系分别如图中的射线OC和ED,当他们行走4小时后,他们之间的距离为3千米.
分析 利用待定系数法求出甲、乙行驶距离s与时间t间函数关系式,令t=4可得二者之间的距离差.
解答 解:根据题意,知OC表示甲行驶距离s与时间t间函数关系,
ED表示表示乙行驶距离s与时间t间函数关系,
设s甲=kt,
由图象可知OC过点(2,4),代入解析式得:2k=4,即k=2,
故s甲=2t,
设s乙=mt+n,
由图象可知,ED过(0,3)、(2,4)两点,
代入解析式得;$\left\{\begin{array}{l}{n=3}\\{2m+n=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=3}\end{array}\right.$,
故s乙=$\frac{1}{2}$t+3,
当t=4时,s甲-s乙=8-5=3(km),
故答案为:3.
点评 此题主要考查了一次函数的应用,结合题意理解函数图象是前提,正确利用待定系数法求出一次函数解析式是解题关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
8.在△ABC中,AB=8,AC=15,BC=17,则该三角形为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰直角三角形 |
12.“三次投掷一枚硬币,三次正面朝上”这一事件是( )
| A. | 必然事件 | B. | 随机事件 | C. | 确定事件 | D. | 不可能事件 |
2.-4+9的相反数是( )
| A. | 5 | B. | -5 | C. | 13 | D. | -13 |
9.已知抛物线y=-x2+2x-3,下列判断正确的是( )
| A. | 开口方向向上,y有最小值是-2 | B. | 抛物线与x轴有两个交点 | ||
| C. | 顶点坐标是(-1,-2) | D. | 当x<1时,y随x增大而增大 |
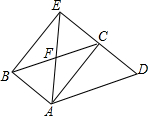 如图,在平行四边形ABCD中,AB=$\sqrt{3}$,AC=3,过点B作BE平行AC交DC的延长线于点E,连结AE,AE交BC于点F,若AB⊥AC,求△ADE的周长.
如图,在平行四边形ABCD中,AB=$\sqrt{3}$,AC=3,过点B作BE平行AC交DC的延长线于点E,连结AE,AE交BC于点F,若AB⊥AC,求△ADE的周长.