题目内容
7.观察下列式子:当n=2时,a=2×2=4,b=22-1=3,c=22+1=5,
当n=3时,a=2×3=6,b=32-1=8,c=32+1=10,
当n=4时,a=2×4=8,b=42-1=15,c=42+1=17,…
根据上述发现的规律,用含n(n≥2的整数)的代数式表示上述特点的勾股数a=2n,b=n2-1,c=n2+1.
分析 通过观察可知a中不变的量有“2”,b中不变的量有“平方减1”,C中不变的量有“平方加1”,故不难得到答案.
解答 解:经过观察可知:a=2n,b=n2-1,c=n2+1.
故答案分别为:2n,n2-1,n2+1.
点评 本题考查的是勾股数,解题的关键是在变化中寻找不变的量,得出规律,通过训练这类题目可以提高观察、分析、解题能力.

练习册系列答案
相关题目
15.方程组$\left\{\begin{array}{l}{x+y=3}\\{x-y=1}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ |
 如图,在数轴上,点A和点B表示的数分别为-$\sqrt{2}$,$\sqrt{7}$,则点A和点B之间表示正整数的点有4个.
如图,在数轴上,点A和点B表示的数分别为-$\sqrt{2}$,$\sqrt{7}$,则点A和点B之间表示正整数的点有4个. 如图,△ABC中,AB=BC,∠ABC=120°,E是线段AC上一点,AE=3EC,连接BE并延长至D,连接CD,若∠BCD=120°,AB=6,则线段CD长为3.
如图,△ABC中,AB=BC,∠ABC=120°,E是线段AC上一点,AE=3EC,连接BE并延长至D,连接CD,若∠BCD=120°,AB=6,则线段CD长为3.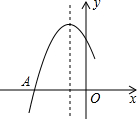 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.与x轴的另一个交点B.给出以下几个结论:①2a-b=0;②b<0;③c>0;④b2>4ac ⑤点B的坐标是(1,0).其中正确结论的序号是①②③④⑤.
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.与x轴的另一个交点B.给出以下几个结论:①2a-b=0;②b<0;③c>0;④b2>4ac ⑤点B的坐标是(1,0).其中正确结论的序号是①②③④⑤. 已知二次函数y=x2-4x.
已知二次函数y=x2-4x.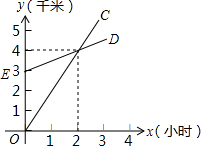 如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们的距离s(千米)与所用的时间t(小时)之间的函数关系分别如图中的射线OC和ED,当他们行走4小时后,他们之间的距离为3千米.
如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们的距离s(千米)与所用的时间t(小时)之间的函数关系分别如图中的射线OC和ED,当他们行走4小时后,他们之间的距离为3千米.