题目内容
5.计算:$\sqrt{18}×\frac{\sqrt{2}}{2}-(\sqrt{3})^{0}$=2.分析 直接利用二次根式的性质化简,进而结合零指数幂的性质求出答案.
解答 解:$\sqrt{18}×\frac{\sqrt{2}}{2}-(\sqrt{3})^{0}$
=3$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-1
=3-1
=2.
故答案为:2.
点评 此题主要考查了二次根式的混合运算以及零指数幂的性质,正确化简二次根式是解题关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.方程组$\left\{\begin{array}{l}{x+y=3}\\{x-y=1}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ |
16. 已知二次函数y=x2-4x.
已知二次函数y=x2-4x.
(1)在给出的直角坐标系内用描点法画出该二次函数的图象;
(2)根据所画的函数图象写出当x在什么范围内时,y≤0?
(3)根据所画的函数图象写出方程:x2-4x=5的解.
 已知二次函数y=x2-4x.
已知二次函数y=x2-4x.(1)在给出的直角坐标系内用描点法画出该二次函数的图象;
(2)根据所画的函数图象写出当x在什么范围内时,y≤0?
(3)根据所画的函数图象写出方程:x2-4x=5的解.
10.式子$\sqrt{1-x}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≤1 | C. | x≥-1 | D. | x≤-1 |
 如图,AB=4,BC=3,AD=13,DC=12,∠B=90°,求四边形ABCD的面积.
如图,AB=4,BC=3,AD=13,DC=12,∠B=90°,求四边形ABCD的面积.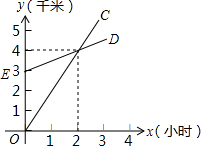 如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们的距离s(千米)与所用的时间t(小时)之间的函数关系分别如图中的射线OC和ED,当他们行走4小时后,他们之间的距离为3千米.
如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们的距离s(千米)与所用的时间t(小时)之间的函数关系分别如图中的射线OC和ED,当他们行走4小时后,他们之间的距离为3千米. “马航失联飞机”牵动世界各国人民的心,许多国家积极组织船只进行搜救.如图,某搜救船在A处望见一可疑物P在北偏东60°方向,同时另一搜救船在B处望见可疑物P在北偏西45°方向.已知AB两处相距800海里,求B处离可疑物P的距离.(结果保留根号)
“马航失联飞机”牵动世界各国人民的心,许多国家积极组织船只进行搜救.如图,某搜救船在A处望见一可疑物P在北偏东60°方向,同时另一搜救船在B处望见可疑物P在北偏西45°方向.已知AB两处相距800海里,求B处离可疑物P的距离.(结果保留根号)