题目内容
 如图所示,∠1=∠2,BD=CD,试证明△ABC是等腰三角形.
如图所示,∠1=∠2,BD=CD,试证明△ABC是等腰三角形.考点:等腰三角形的判定
专题:证明题
分析:由BD=CD可得到∠DBC=∠DCB,再结合条件证明∠ABC=∠ACB即可.
解答:证明:∵BD=CD,
∴∠DBC=∠DCB,
∵∠1=∠2,
∴∠1+∠DBC=∠2+∠DCB,
即∠ABC=∠ACB,
∴AB=AC,
即△ABC是等腰三角形.
∴∠DBC=∠DCB,
∵∠1=∠2,
∴∠1+∠DBC=∠2+∠DCB,
即∠ABC=∠ACB,
∴AB=AC,
即△ABC是等腰三角形.
点评:本题主要考查等腰三角形的判定和性质,掌握等边对等角、等角对等边是解题的关键.

练习册系列答案
相关题目
如果直角三角形的三条边长分别是3,4,x,那么x的值为( )
| A、4 | ||
| B、5 | ||
C、4或
| ||
D、5或
|
 如图,AB,BC,AC表示的是三条河流,现决定在这三条河流中间修建一个木材厂,使该厂到三条河流的距离相等,以便利用走水路向外运木柴,则这个木柴长应建在( )
如图,AB,BC,AC表示的是三条河流,现决定在这三条河流中间修建一个木材厂,使该厂到三条河流的距离相等,以便利用走水路向外运木柴,则这个木柴长应建在( )| A、AC,BC两边高线的交点处 |
| B、AC,BC两边中线的交点处 |
| C、AC,BC两边垂直平分线的交点处 |
| D、∠A,∠B两角的平分线的交点处 |
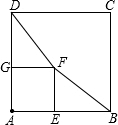 已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.如图,连结DF、BF.
已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.如图,连结DF、BF.