题目内容
4. 如图所示,BD是△ABC的角平分线,DE垂直平分BC,若∠A=120°,则∠C的度数为( )
如图所示,BD是△ABC的角平分线,DE垂直平分BC,若∠A=120°,则∠C的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 先由角平分线的性质得出∠ABD=∠DBC,再由线段垂直平分线的性质及等边对等角得出∠C=∠DBC,根据直角三角形的性质得出∠ACB度数.
解答 解:∵BD是∠ABC的角平分线,
∴∠ABD=∠DBC,
又∵DE是BC的垂直平分线,
∴CD=DB,
∴∠C=∠DBC,
∴∠C=∠DBC=∠ABD,
又∵在Rt△ABC中,∠A=120°,且∠A+∠ACB+∠ABD+∠DBC=180°,
∴∠ACB=∠DBC=∠ABD=20°.
故选B.
点评 本题考查的是线段垂直平分线及角平分线的性质,解答此类题目时往往用到三角形的内角和是180°这一隐藏条件.

练习册系列答案
相关题目
15.将正整数依次按如表规律排成4列,根据表中的排列规律,数2016应在( )
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
| A. | 第671行第2列 | B. | 第671行第3列 | C. | 第672行第2列 | D. | 第672行第3列 |
19.圆锥体的底面半径为2,全面积为12π,则其侧面展开图的圆心角为( )
| A. | 90° | B. | 120° | C. | 150° | D. | 180° |
16.下列计算正确的是( )
| A. | 5a+2a=7a2 | B. | 5a-2a=3 | C. | 5a-2a=3a | D. | -ab+2ab2=ab2 |
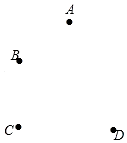 如图,平面上四个点A,B,C,D.按要求完成下列问题:
如图,平面上四个点A,B,C,D.按要求完成下列问题: