题目内容
3.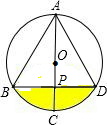 如图,已知在⊙O中,AB=4$\sqrt{3}$,AF=6,AC是直径,AC⊥BD于F,图中阴影部分的面积是( )
如图,已知在⊙O中,AB=4$\sqrt{3}$,AF=6,AC是直径,AC⊥BD于F,图中阴影部分的面积是( )| A. | $\frac{8}{3}$π-2$\sqrt{3}$ | B. | $\frac{16}{3}$π-2$\sqrt{3}$ | C. | $\frac{8}{3}$π-4$\sqrt{3}$ | D. | $\frac{16}{3}$π-4$\sqrt{3}$ |
分析 利用勾股定理求得BD=2BF=4$\sqrt{3}$,连接OB、OD、BC,先求得∠ABC=90°,进而根据射影定理求得FC=2,从而求得直径的长,根据余弦函数求得∠BAF=30°,进而得出∠BOD=120°,最后根据S阴影=S扇形-S△BOD即可求得阴影的面积.
解答 解:∵AC是直径,AC⊥BD于F,
∴BF=DF,$\widehat{BC}$=$\widehat{DC}$,
∴∠BAC=∠DAC,
在RT△ABF中,BF=$\sqrt{A{B}^{2}-A{F}^{2}}$=2$\sqrt{3}$,
∴BD=2BF=4$\sqrt{3}$,
连接OB、OD、BC,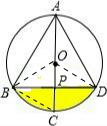 ∵AC是直径,
∵AC是直径,
∴∠ABC=90°,
∴BF2=AF•FC,即(2$\sqrt{3}$)2=6FC,
∴FC=2,
∴直径AC=AF+FC=6+2=8,
∴⊙O的半径为4,
∵AB=4$\sqrt{3}$,AF=6,
∴cos∠BAF=$\frac{AF}{AB}$=$\frac{6}{4\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∴∠BAF=30°,
∴∠BAD=60°,
∴∠BOD=120°,
∵OC=4,FC=2,
∴OF=2,
∴S阴影=S扇形-S△BOD=$\frac{120π×{4}^{2}}{360}$-$\frac{1}{2}$×4$\sqrt{3}$×2=$\frac{16}{3}$π-4$\sqrt{3}$;
故选D.
点评 本题考查了垂径定理,扇形的面积、及直角三角函数和勾股定理等知识,难度适中.

练习册系列答案
相关题目
15.x与6的和一半是非负数,用不等式表示为( )
| A. | $\frac{1}{2}$(x+6)≥0 | B. | $\frac{1}{2}$x+6≤0 | C. | $\frac{1}{2}$x+6≥0 | D. | $\frac{1}{2}$(x+6)≤0 |
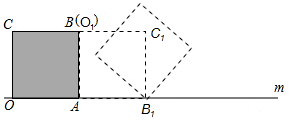
12. 下列四幅图案中,能通过平移左图所示的图案得到的是( )
下列四幅图案中,能通过平移左图所示的图案得到的是( )
 下列四幅图案中,能通过平移左图所示的图案得到的是( )
下列四幅图案中,能通过平移左图所示的图案得到的是( )| A. |  | B. |  | C. |  | D. |  |
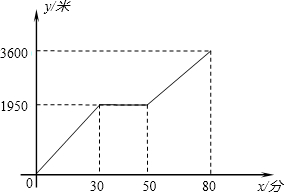 小华和小晶上山游玩,小华步行,小晶乘坐缆车,相约在山顶缆车的终点会合.已知小华步行的路程是缆车所经线路长的2倍,小晶在小华出发后50分钟才坐上缆车,缆车的平均速度为每分钟180米.图中的折线反映了小华行走的路程y(米)与时间x(分钟)之间的函数关系.
小华和小晶上山游玩,小华步行,小晶乘坐缆车,相约在山顶缆车的终点会合.已知小华步行的路程是缆车所经线路长的2倍,小晶在小华出发后50分钟才坐上缆车,缆车的平均速度为每分钟180米.图中的折线反映了小华行走的路程y(米)与时间x(分钟)之间的函数关系.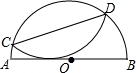 半圆⊙O中,AB为直径,C、D为半圆上任意两点,将$\widehat{CD}$沿直线CD翻折使AB与$\widehat{CD}$相切,已知AB=8,求CD的最大值4$\sqrt{3}$.
半圆⊙O中,AB为直径,C、D为半圆上任意两点,将$\widehat{CD}$沿直线CD翻折使AB与$\widehat{CD}$相切,已知AB=8,求CD的最大值4$\sqrt{3}$.