题目内容
10．化简代数式：（$\frac{3}{x+1}$-x+1）÷$\frac{{x}^{2}+4x+4}{x+1}$．分析 根据分式的运算即可求出答案．
解答 解：原式=$\frac{3-（x-1）（x+1）}{x+1}$×$\frac{x+1}{（x+2）^{2}}$
=$\frac{4-{x}^{2}}{（x+2）^{2}}$
=$-\frac{（x+2）（x-2）}{（x+2）^{2}}$
=-$\frac{x-2}{x+2}$
点评 本题考查分式的运算，解题的关键是熟练运用分式的运算法则，本题属于基础题型．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
如图，在△ABC中，AB=AC，AB的垂直平分线交AC于点E，垂足为D．若△ABC的周长为20cm，△BCE的周长为12cm，求BC的长．
15．下列计算正确的是（ ）
| A． | $\frac{{\sqrt{27}}}{3}=9$ | B． | $（\sqrt{2}+\sqrt{5}{）^2}=7$ | C． | $\sqrt{（\sqrt{3}-2{）^2}}=\sqrt{3}-2$ | D． | $\sqrt{12}-\sqrt{3}=\sqrt{3}$ |
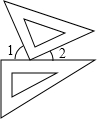一副三角板按如图方式摆放，且∠1的度数比∠2的度数大50°，若设∠1=x°，∠2=y°，请列方程组求x，y的值．