题目内容
19.计算:$\sqrt{32}$-$\frac{1}{\sqrt{3}+\sqrt{2}}$+3$\sqrt{\frac{1}{3}}$.分析 首先化简二次根式以及分母有理化,进而合并同类二次根式即可.
解答 解:$\sqrt{32}$-$\frac{1}{\sqrt{3}+\sqrt{2}}$+3$\sqrt{\frac{1}{3}}$
=4$\sqrt{2}$-$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$+$\sqrt{3}$
=4$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$+$\sqrt{3}$
=5$\sqrt{2}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
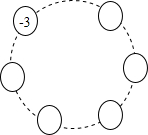 如图,请在小圆圈内填满数,使每个小圆圈里的数都是它两旁小圆圈里数的和,并求出所有小圆圈里数的和,如果把原来填的-3改成a,按上面的要求填满后,所有小圆圈里数的和又是多少?
如图,请在小圆圈内填满数,使每个小圆圈里的数都是它两旁小圆圈里数的和,并求出所有小圆圈里数的和,如果把原来填的-3改成a,按上面的要求填满后,所有小圆圈里数的和又是多少?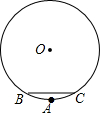 如图,某健身广场中心修建了一个圆形喷水池,数学活动小组为测量喷水池的半径,选取水池围栏上的A,B,C三根白玉石柱,量得AB=AC,BC长为14m,点A到BC的距离为1m,请你帮他们求出喷水池的半径.
如图,某健身广场中心修建了一个圆形喷水池,数学活动小组为测量喷水池的半径,选取水池围栏上的A,B,C三根白玉石柱,量得AB=AC,BC长为14m,点A到BC的距离为1m,请你帮他们求出喷水池的半径. 如图是抛物线形拱桥,当水面在l时.拱顶离水面2m.水面宽8m.水面下降0.25m.水面宽度增加多少?
如图是抛物线形拱桥,当水面在l时.拱顶离水面2m.水面宽8m.水面下降0.25m.水面宽度增加多少?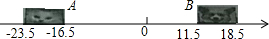 七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题:
七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题: