题目内容
14.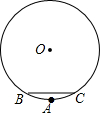 如图,某健身广场中心修建了一个圆形喷水池,数学活动小组为测量喷水池的半径,选取水池围栏上的A,B,C三根白玉石柱,量得AB=AC,BC长为14m,点A到BC的距离为1m,请你帮他们求出喷水池的半径.
如图,某健身广场中心修建了一个圆形喷水池,数学活动小组为测量喷水池的半径,选取水池围栏上的A,B,C三根白玉石柱,量得AB=AC,BC长为14m,点A到BC的距离为1m,请你帮他们求出喷水池的半径.
分析 连接半径OA、OB、OC,设OB交AC于点D.根据垂径定理的推论,得OA⊥BC,BD=CD=7m.设OA=x米,根据勾股定理即可求解.
解答  解:连接半径OA、OB、OC,设OB交AC于点D.
解:连接半径OA、OB、OC,设OB交AC于点D.
∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴OA⊥BC,
∴∠AOB=∠AOC,
∵OB=OC,
∴BD=CD=7m.
设OA=xm,则有x2-(x-1)2=72,
解得x=25m.
故喷水池的半径为25m.
点评 此题考查了垂径定理的应用,用到的知识点是等弦对等弧、垂径定理的推论、勾股定理,关键是根据题意作出辅助线,构造直角三角形.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3.一个多边形的边数是9,则它的内角和为( )
| A. | 1260° | B. | 1080° | C. | 900° | D. | 720° |

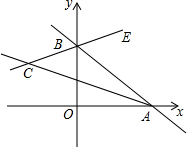 如图,在平面直角坐标系中,已知点A,点B分别是x,y轴的正半轴上的动点,BE是∠ABy的平分线.BE的反向处长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否会发生变化?如果变化,说明你的理由;如果不变,求出∠ACB的度数.
如图,在平面直角坐标系中,已知点A,点B分别是x,y轴的正半轴上的动点,BE是∠ABy的平分线.BE的反向处长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否会发生变化?如果变化,说明你的理由;如果不变,求出∠ACB的度数. 请把如图所示的图形缩小2倍.
请把如图所示的图形缩小2倍. 将-8,-4,-2,2,4,8这6个数分别填入下图的6个方格内,使得处于同一横行,同一竖列、同一斜对角线上的3个数相加加都得0.
将-8,-4,-2,2,4,8这6个数分别填入下图的6个方格内,使得处于同一横行,同一竖列、同一斜对角线上的3个数相加加都得0.