题目内容
一个三位数，百位上的数与其后的二位数之和为58．若把百位上的数移作个位上的数，并把原来十位和个位上的数顺次升为百位和十位上的数，则新的三位数比原数大306．求原来这个三位数．
考点：一元一次方程的应用
专题：
分析：设百位上的数字为x，则原来三位数是100x+（58-x），新三位数是10（58-x）+x，根据题意列出一元一次方程，解出x即可．
解答：解：设百位上的数字为x，
原来三位数是100x+（58-x），新三位数是10（58-x）+x，
根据题意得：
10（58-x）+x-[100x+（58-x）]=306，
整理得：108x=216，
解得x=2，
即原来三位数是256，
答：原来三位数是256．
原来三位数是100x+（58-x），新三位数是10（58-x）+x，
根据题意得：
10（58-x）+x-[100x+（58-x）]=306，
整理得：108x=216，
解得x=2，
即原来三位数是256，
答：原来三位数是256．
点评：本题考查了一元一次方程的应用，解答本题的关键是设出未知数，表示三个数位上的数字，此题难度不大．
练习册系列答案
相关题目
如图，把一台电视机（底面为矩形ABCD）放置于墙角的电视柜（其桌面为矩形EFGH）上，若∠BAF=30°，电视机长AD=62厘米，则DG的长为
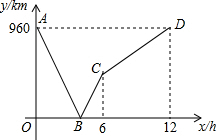一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发．设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．根据题中所给信息解答：当出发几个小时后，两车相距为240km？（ ）
如图，在平行四边形ABCD中，E是BC中点，AF⊥CD于点F，AE=4，AF=6，则△AEF的面积是
画出如图主视图、俯视图、左视图．
在数轴上画出表示