题目内容
6.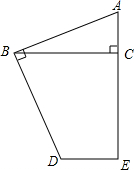 如图,∠ABD=90°,AB=BD,∠ACB=90°,∠CED=90°,BC=10cm.线段BC⊥AE,求四边形ABDE的面积.
如图,∠ABD=90°,AB=BD,∠ACB=90°,∠CED=90°,BC=10cm.线段BC⊥AE,求四边形ABDE的面积.
分析 过点D作DF⊥BC,垂足为F,可证明△ABC≌△BDF,得出DF=10,设AC=x,则BF=x,四边形DECF为矩形,CF=10-x,把△ABC,△BDF,矩形DECF的面积加起来即为四边形ABDE的面积.
解答 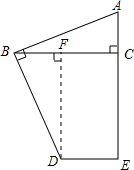 解:过点D作DF⊥BC,垂足为F,
解:过点D作DF⊥BC,垂足为F,
∵∠ABD=90°,∠ACB=90°,
∴∠ABC=∠BDF,
在△ABC△DBF中,
$\left\{\begin{array}{l}{∠ACB=∠BFD}\\{ABC=∠BDF}\\{AB=BD}\end{array}\right.$,
∴△ABC≌△BDF,
∴AC=BF,BC=DF,
∵BC=10,
∴DF=10,
设AC=x,则BF=x,
∵∠CED=90°,
∴四边形DECF为矩形,
∴CF=10-x,
∴S四边形ABDE=S△ABC+S△BDF+S矩形DECF=10x+10(10-x)=100.
点评 本题考查了全等三角形的性质和判定以及矩形的判定和性质,把不规则的图形转化为规则图形是解题的关键.

练习册系列答案
相关题目
15.已知直角三角形的一个锐角为60°,斜边长为1,那么此直角三角形的面积是( )
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2$\sqrt{3}$ |
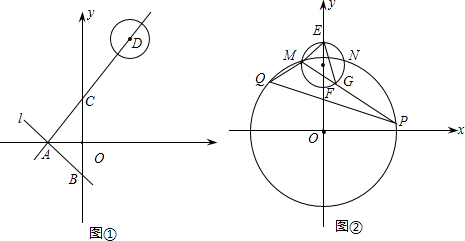
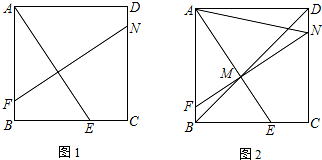
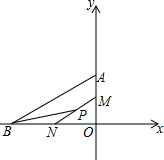 如图,在平面直角坐标系中,点A的坐标为(0,5),点B的坐标为(-8,0),点M从点A出发沿AO以每秒1个单位长度的速度运动至点O,同时点N从点B出发沿射线BO以每秒2个单位长度的速度运动,当点M运动至O时,点N也同时停止运动,P是MN的中点,连接BP,设点M的运动时间为t(s).
如图,在平面直角坐标系中,点A的坐标为(0,5),点B的坐标为(-8,0),点M从点A出发沿AO以每秒1个单位长度的速度运动至点O,同时点N从点B出发沿射线BO以每秒2个单位长度的速度运动,当点M运动至O时,点N也同时停止运动,P是MN的中点,连接BP,设点M的运动时间为t(s).