Question

16．如图，已知A，B，C分别是⊙O上的点，∠B=60°，P是直径CD的延长线上的一点，且AP=AC．
（1）求证：AP与⊙O相切；
（2）如果AC=3，求PD的长．

Answer 1

分析 （1）连结OA、AD，如图，利用圆周角定理得到∠CAD=90°，∠ADC=∠B=60°，则∠ACD=30°，再利用AP=AC得到∠P=∠ACD=30°，接着根据圆周角定理得∠AOD=2∠ACD=60°，然后根据三角形内角和定理可计算出∠OAP=90°，于是根据切线的判定定理可判断AP与⊙O相切；
（2）在Rt△OPA中利用含30度的直角三角形三边的关系得到OA=$\frac{\sqrt{3}}{3}$AP=$\sqrt{3}$，PO=2OA=2$\sqrt{3}$，然后计算PO-OD即可．

解答 （1）证明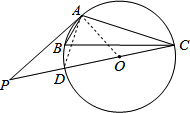：连结OA、AD，如图，
∵CD为直径，
∴∠CAD=90°，
∵∠ADC=∠B=60°，
∴∠ACD=30°，
∵AP=AC，
∴∠P=∠ACD=30°，
∵∠AOD=2∠ACD=60°，
∴∠OAP=180°-60°-30°=90°，
∴OA⊥PA，
∴AP与⊙O相切；
（2）解：PA=AC=2，
在Rt△OPA中，∵∠P=30°，
∴OA=$\frac{\sqrt{3}}{3}$AP=$\sqrt{3}$，
∵PO=2OA=2$\sqrt{3}$，
∴PD=PO-OD=2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$．

点评 本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．记住含30度的直角三角形三边的关系．