题目内容
已知抛物线 y=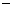 mx2+4x+2m与x轴交于点A(
mx2+4x+2m与x轴交于点A(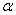 ,0)、B(
,0)、B(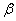 ,0),且
,0),且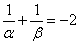 .
.
(1)求抛物线的解析式.
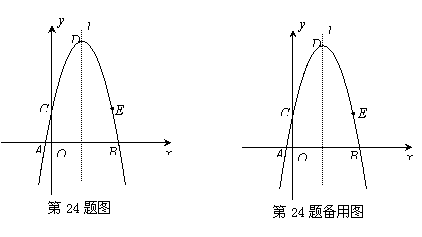
(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l对称点为E.是否存在 x轴上的点M、y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形为平行四边形时,求点P的坐标.
 |
 (1)由题意可知,
(1)由题意可知,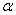 ,
,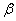 是方程
是方程 的两根,由根与系数的关系可得,
的两根,由根与系数的关系可得,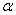 +
+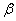 =
= ,
,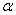
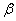 =-2.
=-2.
∵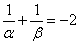 ,
,
∴ .即:
.即: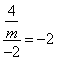 .
.
∴m=1.
∴抛物线解析式为 .
.
(2) 存在x轴,y轴上的点M,N,使得四边形DNME的周长最小.
∵ ,
,
∴抛物线的对称轴 为
为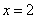 ,顶点D的坐标为(2,6).
,顶点D的坐标为(2,6).
又抛物线与y轴交点C的坐标为(0,2),点E与点C关于 对称,
对称,
∴E点坐标为(4,2).
作点D关于y轴的对称点D′,作点E关于x轴的对称点E′,
则D′坐标为(-2,6),E′坐标为(4,-2).连接D′E′,交x轴于M,交y轴与N.
此时,四边形DNME的周长最小为D′E′+DE.(如图1所示)
延长E′E, D′D交于一点F,在Rt△D′E′F中,D′F=6,E′F=8.
∴D′E′=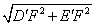 =
= .
.
 设对称轴
设对称轴 与CE交于点G,在Rt△DG E中,DG=4,EG=2.
与CE交于点G,在Rt△DG E中,DG=4,EG=2.
∴DE=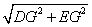 =
=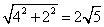 .
.
∴四边形DNME的周长的最小值为
10+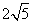 .
.
(3)如图2, P为抛物线上的点,过P作PH⊥x轴,垂足为H.若以点D、E、P、Q为顶点的四边形为平行四边形,则△PHQ≌△DGE.
∴PH=DG=4.
即 =4.
=4.
∴当y= 4时,
4时,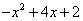 =4,解得
=4,解得
当y=-4时,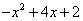 =-4,解得
=-4,解得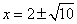 .
.
∴点P的坐标为( ,4),(
,4),( ,4),(
,4),( ,-4),(
,-4),( ,-4).
,-4).

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案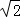 =1.41)
=1.41)
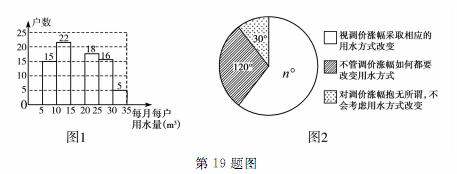
 上运动,设△APO的面积
上运动,设△APO的面积 为S,则下面能够反映S与m的函数关系的图象是
为S,则下面能够反映S与m的函数关系的图象是
 B.
B.  C.
C.  D.
D. 

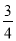 x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
 x2 向左平移8个单位,再向下平移9个单位后,所得抛物线的表达式是 .
x2 向左平移8个单位,再向下平移9个单位后,所得抛物线的表达式是 .