题目内容
2.代数式4ab-3a2-5b2+4a-8b-5的最大值是13.分析 多项式配方变形后,利用非负数的性质求出多项式的最大值.
解答 解:∵4ab-3a2-5b2+4a-8b-5=(4ab-a2-4b2)+(-2a2+4a-2)+(-b2-8b-16)+13=-(a-2b)2-2(a-1)2-(b+4)2+13=-[(a-2b)2+2(a-1)2+(b+4)2]+13,
∵-[(a-2b)2+2(a-1)2+(b+4)2]≤0,
∴-[(a-2b)2+2(a-1)2+(b+4)2]+13≤13,
∴4ab-3a2-5b2+4a-8b-5的最大值是13,
故答案为:13.
点评 此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
7. 某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示.
某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示.
根据录用程序,组织200名职工对三人利用投标推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如图所示,每得一票记作1分.
(1)甲的民主评议得分为50分;如果根据三项测试的平均成绩确定录用人选,那么乙将被录用.
(2)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的比例确定个人成绩,那么谁将被录用?(请写出计算过程)
 某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示.
某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示.| 测试 项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
(1)甲的民主评议得分为50分;如果根据三项测试的平均成绩确定录用人选,那么乙将被录用.
(2)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的比例确定个人成绩,那么谁将被录用?(请写出计算过程)
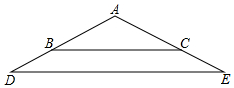 在等腰三角形ABC和等腰三角形ADE中,∠BAC=∠DAE=120°,AB=2,AD=3,点A、B、D在同一条直线上,将△ADE绕点A旋转180°,在旋转过程中,直线BD、CE的交点为点F,直接写出点F经过的路径的长度4π.
在等腰三角形ABC和等腰三角形ADE中,∠BAC=∠DAE=120°,AB=2,AD=3,点A、B、D在同一条直线上,将△ADE绕点A旋转180°,在旋转过程中,直线BD、CE的交点为点F,直接写出点F经过的路径的长度4π. 如图,在?ABCD中,AC⊥CD,E是AD的中点,若CE=4,则BC的长是8.
如图,在?ABCD中,AC⊥CD,E是AD的中点,若CE=4,则BC的长是8. 如图,在直角坐标系中,直线l是经过点(0,1)且平行于x轴的直线,则点(2,-2)关于直线l的对称点的坐标为(2,4).
如图,在直角坐标系中,直线l是经过点(0,1)且平行于x轴的直线,则点(2,-2)关于直线l的对称点的坐标为(2,4).