题目内容
12．已知m、n都是方程x2+2014x+2015=0的根，则代数式（m2+2014m-2015）（n2+2014n+2014）=4030．分析 由于m、n是方程x2+2014x+2015=0的根，可得m2+2014m、n2+2014n的值，然后把m2+2014m、n2+2014n的值整体代入所求代数式计算即可．
解答 解：∵m、n都是方程x2+2014x+2015=0的根，
∴m2+2014m+2015=0，n2+2014n+2015=0，
即m2+2014m=-2015，n2+2014n=-2015，
∴原式=（-2015-2015）×（-2015+2014）=4030，
故答案为：4030．
点评 本题考查了一元二次方程的解的意义：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解，解题的关键是整体代入．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
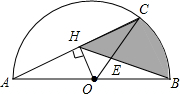如图，AB为半圆的直径，弧AC为弧CB的两倍，OH⊥AC于点H，BH与OC交于E，己知AC=2$\sqrt{3}$．
如图，是反比例函数y=$\frac{6}{x}$和y=$\frac{4}{x}$在第一象限的图象，点P是函数y=$\frac{6}{x}$图象上的一点，过点P作PA∥x轴，PB∥y轴，并分别交函数y=$\frac{4}{x}$的图象于A，B两点，则四边形OAPB的面积为（ ）