题目内容
20.某种商品每件的进价为30元,在某段时间内若以每件x元出售(30<x<100),可卖出(100-x),应如何定价才能使利润最大?最大利润是多少?分析 本题是营销问题,基本等量关系:利润=每件利润×销售量,每件利润=每件售价-每件进价,再根据所列二次函数求最大值.
解答 解:设最大利润为w元,
则w=(x-30)(100-x)=-(x-65)2+1225,
∵-1<0,0<x<100,
∴当x=65时,二次函数有最大值1225,
∴定价是65元时,利润最大.
点评 本题考查了把实际问题转化为二次函数,再利用二次函数的性质进行实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
8.数轴上与原点距离小于3.5个单位长度的整数点的个数是( )
| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
15.如果一个一元二次方程的根有两个相等的实数根,那么这个方程可以是( )
| A. | x2+2x=0 | B. | (x-1)2=0 | C. | x2=1 | D. | x2+1=0 |
9.下列说法不正确的是( )
| A. | 近似数0.5和0.50的精确度不同 | |
| B. | 近似数5.61×104精确到百分位 | |
| C. | 65800精确到万位是7×104 | |
| D. | 近似数1.8是由a四舍五入得到的,则a的取值范围是1.75≤a<1.85 |
10.为筹备首届青运会,福州市共投入了219800万元人民币建造各项体育设施,用科学记数法表示该数据是( )
| A. | 2.918×105元 | B. | 2.918×106元 | C. | 2.918×109元 | D. | 2.918×1010元 |
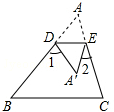 如图,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED内部A′处,已知∠A=40°,则∠1+∠2=80°度.
如图,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED内部A′处,已知∠A=40°,则∠1+∠2=80°度.