题目内容
 如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDA的度数等于( )
如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDA的度数等于( )| A、70° | B、100° |
| C、110° | D、120° |
考点:平行线的性质
专题:
分析:由平行可求得∠CDE,结合条件可求得∠CDA.
解答:解:
∵DE∥AC,
∴∠CDE=∠C=50°,
又∠CDA+∠CDE+∠BDE=180°,
∴∠CDA=180°-50°-60°=70°,
故选A.
∵DE∥AC,
∴∠CDE=∠C=50°,
又∠CDA+∠CDE+∠BDE=180°,
∴∠CDA=180°-50°-60°=70°,
故选A.
点评:本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
 如图,正五边形ABCDE内接于⊙O,连接对角线AC,AD,则下列判断中错误的是( )
如图,正五边形ABCDE内接于⊙O,连接对角线AC,AD,则下列判断中错误的是( )| A、BC∥AD |
| B、∠BAE=3∠CAD |
| C、△BAC≌△EAD |
| D、AC=2CD |
 有一个数值转换器,其工作原理如图所示,若输入2,则输出的结果是( )
有一个数值转换器,其工作原理如图所示,若输入2,则输出的结果是( )| A、-8 | B、-6 | C、8 | D、10 |
下列说法正确的是( )
| A、射线PA和射线AP是同一条射线 |
| B、射线OA的长度是12cm |
| C、直线ab、cd相交于点M |
| D、两点确定一条直线 |
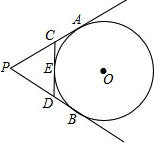 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,若⊙O的半径为r,△PCD的周长等于3r,则tan
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,若⊙O的半径为r,△PCD的周长等于3r,则tan 如图,在?ABCD中,AC⊥DC,且AD=10,AB=8,则OC=
如图,在?ABCD中,AC⊥DC,且AD=10,AB=8,则OC= 如图,在△ABC中,AB=8,AC=5,AD是△ABC的中线,求AD的取值范围.
如图,在△ABC中,AB=8,AC=5,AD是△ABC的中线,求AD的取值范围.