题目内容
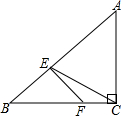
3.已知,如图1,在?ABCD中,∠DAC=90°,∠CAB=30°,以AD为边在?ABCD的内部作等腰△EAD,ED=EA,∠EAD=30°,AE=2$\sqrt{3}$.(1)求△EAD的面积.
(2)若△EAD以每秒2个长度单位的速度沿DC方向向右平行移动,得到△E0A0D0,设运动时间为t秒,当点E0刚好落在AC上时,求运动时间t.
(3)如图2,在(2)中,当△EAD停止移动后得到△EBC,将△EBC绕点E按逆时针方向旋转α(0°<α<60°),在旋转过程中,B的对应点为B1,C的对应点为C1,B1C1分别与BC,BE交于G,H两点,BC与EC1交于点F,是否存在这样的α,使△C1FG为等腰三角形?若存在,求出α的度数和FG的长度;若不存在,请说明理由.
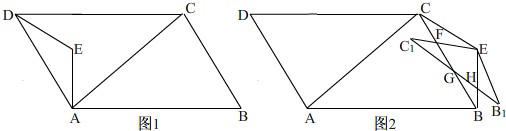
分析 (1)先构造出直角三角形,得出有一个锐角为30°的直角三角形,求出AD,根据三角形的面积公式直接得出;
(2)先判断出∠EAB是直角,由平移得出∠AA0E0=90°,在含有30°的直角三角形中求出EE0即可;
(3)分三种讨论计算,前两种情况不满足0°<α<60°,只有第三种情况满足,再构造直角三角形求出即可.
解答 解:(1)如图,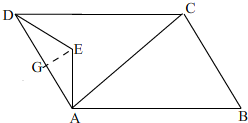
过点E作EG⊥AD,
∵ED=EA,
∴AD=2AG,
在Rt△AGE中,ED=EA,∠EAD=30°,AE=2$\sqrt{3}$,
∴EG=$\sqrt{3}$,AG=3,
∴AD=2AG=6,
∴S△ADE=$\frac{1}{2}$AD×EG=$\frac{1}{2}$×6×$\sqrt{3}$=3$\sqrt{3}$;
(2)如图2,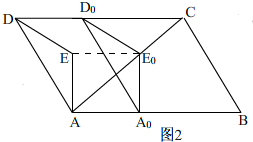
∵∠CAD=90°,∠DAE=30°,
∴∠CAE=60°,
∵∠CAB=30°,
∴∠BAE=90°,
由平移知,A0E0=AE=2$\sqrt{3}$,EE0=AA0,∠AA0E0=90°,
∴AA0=$\sqrt{3}$A0E0=6,
∴EE0=6,
∴t=6÷2=3;
(3)如图3,由平移得,CE=2$\sqrt{3}$,∠BCE=30°,
由旋转知,∠EC1B1=30°,
∵△C1FG为等腰三角形,
①当C1F=C1G时,∠C1FG=∠C1GF=$\frac{1}{2}$(180°-∠EC1B1)=75°,
∴∠CFE=75°,
∵∠BCE=30°,
根据三角形的内角和得,∠CEF=75°,
∵△EBC绕点E按逆时针方向旋转α(0°<α<60°),
∴此种情况不符合题意,舍去,
②当GC1=GF时,∠GFC1=∠EC1B1=30°,
∴∠CFE=30°,
根据三角形内角和得,∠CEF=180°-∠ECB-∠CFE=120,
∵△EBC绕点E按逆时针方向旋转α(0°<α<60°),
∴此种情况不符合题意,舍去,
③当FC1=FG时,∠C1GF=∠EC1B1=30°,
∴∠CFE=∠C1FG=180°-∠C1GF-∠EC1B1=120°,
根据三角形内角和得,∠CEF=30°,
∴FC=FE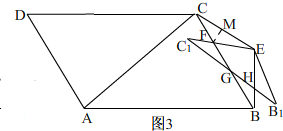
过点F作FM⊥CE,
∴ME=$\frac{1}{2}$CE=$\sqrt{3}$,
在Rt△EFM中,∠FEM=30°,ME=$\sqrt{3}$,
∴EF=2,
∴FC1=C1E-EF=CE-EF=2$\sqrt{3}$-2,
∴FG=FC1=2$\sqrt{3}$-2.
点评 此题是几何变换综合题,主要考查了等腰三角形的性质,三角形的内角和定理,平移和旋转的性质,解本题的关键是判断出∠EAB=90°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -1或11 | B. | 1或-11 | C. | -1或-11 | D. | 11 |
| A. | a≥b | B. | a≤b | C. | a>b | D. | a<b |
| A. | 0.002精确到千分位,有一个有效数字 | |
| B. | 200精确到个位,有一个有效数字 | |
| C. | 29.6精确到十分位,有三个有效数字 | |
| D. | 29.60精确到百分位,有四个有效数字 |
 如图,在△ABC中,AC=BC,∠BCA=90°,点E是斜边AB上的一点,作EF⊥AB交边BC于点F连结EC,若BE:EA=1:2,则∠ECF的余弦值为( )
如图,在△ABC中,AC=BC,∠BCA=90°,点E是斜边AB上的一点,作EF⊥AB交边BC于点F连结EC,若BE:EA=1:2,则∠ECF的余弦值为( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\sqrt{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
 如图所示为沱江两个风景区的位置,若麻拐岩风景区的坐标为(-4,2),则阳华岩风景区的坐标为(0,-3).
如图所示为沱江两个风景区的位置,若麻拐岩风景区的坐标为(-4,2),则阳华岩风景区的坐标为(0,-3).