题目内容
2. 如图:已知∠DAE=∠CBE,EA=EB,求证:△ABD≌△BAC.
如图:已知∠DAE=∠CBE,EA=EB,求证:△ABD≌△BAC.
分析 由EA=EB可求得∠EAB=∠EBA,结合条件证明△ABD≌△BAC.
解答 证明:
∵EA=EB,
∴∠EAB=∠EBA,
∵∠DAE=∠CBE,
∴∠DAB=∠CBA,
在△ABD和△BAC中
$\left\{\begin{array}{l}{∠DAB=∠CBA}\\{AB=BA}\\{∠DBA=∠CAB}\end{array}\right.$
∴△ABD≌△BAC(ASA).
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和性质(即全等三角形的对应边相等、对应角相等)是解题的关键.

练习册系列答案
相关题目
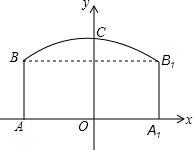 如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系.
如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系.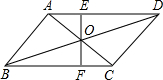 已知:?ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F,求证:OE=OF.
已知:?ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F,求证:OE=OF.