Question

在△ABC中，AB=15，AC=13，高AD=12，则△ABC的周长是（ ）

A、42 B、32 C、42或32 D、37或33

Answer 1

C．

【解析】

试题分析：此题应分两种情况说明：

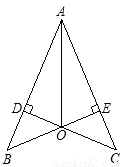
（1）当△ABC为锐角三角形时，如图：

在Rt△ABD中，

BD=，

在Rt△ACD中，

CD=

∴BC=5+9=14

∴△ABC的周长为：15+13+14=42；

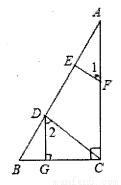
（2）当△ABC为钝角三角形时，如图：

在Rt△ABD中，BD=，

在Rt△ACD中，CD=，

∴BC=9-5=4．

∴△ABC的周长为：15+13+4=32

∴当△ABC为锐角三角形时，△ABC的周长为42；当△ABC为钝角三角形时，△ABC的周长为32．

综上所述，△ABC的周长是42或32．

故选C．

考点：勾股定理．