题目内容
证明题(本题8分,每空1分)
已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
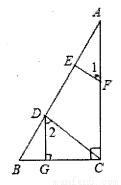
证明:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义),
∴DG//AC(___________________________________),
∴∠2=_______(___________________________________),
∵∠1=∠2(______________),
∴∠1=∠DCA(等量代换),
∴EF//CD(___________________________________),
∴∠AEF=∠ADC(__________________________________),
∵EF⊥AB(已知)
∴∠AEF=90°(___________________________________),
∴∠ADC=90°
∴CD⊥AB(___________________________________).
同旁内角互补两直线平行;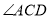 ;两直线平行,内错角相等;已知;同位角相等,两直线平行;两直线平行,同位角相等;垂直的定义;垂直的定义.
;两直线平行,内错角相等;已知;同位角相等,两直线平行;两直线平行,同位角相等;垂直的定义;垂直的定义.
【解析】
试题分析:首先证得DG//AC,再应用平行线的判定证得EF//CD,进一步证得∠ADC=90°,即CD⊥AB.
试题解析:证明:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义),
∴DG//AC(同旁内角互补两直线平行),
∴∠2=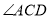 (两直线平行,内错角相等),
(两直线平行,内错角相等),
∵∠1=∠2(已知),
∴∠1=∠DCA(等量代换),
∴EF//CD(同位角相等,两直线平行),
∴∠AEF=∠ADC(两直线平行,同位角相等),
∵EF⊥AB(已知)
∴∠AEF=90°(垂直的定义),
∴∠ADC=90°
∴CD⊥AB(垂直的定义).
故答案为:同旁内角互补两直线平行;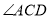 ;两直线平行,内错角相等;已知;同位角相等,两直线平行;两直线平行,同位角相等;垂直的定义;垂直的定义.
;两直线平行,内错角相等;已知;同位角相等,两直线平行;两直线平行,同位角相等;垂直的定义;垂直的定义.
考点:平行线的判定和性质;垂直的定义.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案不等式组 的解集是( )[中&国教^育出%@版~网]
的解集是( )[中&国教^育出%@版~网]
|
| A. | x>1 | B. | x<2 | C. | 1≤x≤2 | D. | 1<x<2 |
 ,求AB的长.
,求AB的长.
 a°,则下列结论: ①∠BOE=
a°,则下列结论: ①∠BOE=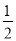 (180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的个数有( )个.
(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的个数有( )个.
 B.
B.
 D.(2xy)3=2x3y
D.(2xy)3=2x3y ;
; ;
; ,
, .
. ,
, 于
于 ,
, 交
交 于
于 ,GE平分∠AEF,则
,GE平分∠AEF,则 是( )
是( )
 B.
B. C.
C. D.
D.