题目内容
如图，∠1=∠2，AB=AD，∠B=∠D，∠3=60，请判断△AEC的形状，并说明理由。
△AEC的形状为等边三角形．理由见解析．
【解析】
试题分析：由∠1=∠2知∠BAC=∠DAE，又AB=AD，∠B=∠D，从而可证△ABC≌△ADE，得：AE=AE．又因为∠3=60，故可判断△AEC的形状为等边三角形．
试题解析：∵∠1=∠2
∴∠1+∠3=∠2+∠3
即：∠BAC=∠DAE
在△ABC和△ADE中
∴△ABC≌△ADE
∴AE=AC
又∠3=60
∴△AEC为等边三角形
考点：等边三角形的判定．
练习册系列答案
发散思维新课堂系列答案
相关题目
（填“＞”或“＜”）
的解互为相反数，则k的值是＿＿＿＿．
，求AB的长．
a°，则下列结论: ①∠BOE＝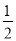
（180-a）°；②OF平分∠BOD；③∠POE＝∠BOF；④∠POB＝2∠DOF．其中正确的个数有（ ）个．