题目内容
16．通分：$\frac{x}{4{x}^{2}-16x+16}$，$\frac{1}{6x-3{x}^{2}}$，$\frac{-2x}{{x}^{2}-4}$．分析 先对原式的分子分母分解因式，然后找出几个分式的最简公分母，然后通分即可解答本题．
解答 解：∵$\frac{x}{4{x}^{2}-16x+16}$=$\frac{x}{4（x-2）^{2}}$，
$\frac{1}{6x-3{x}^{2}}$=$\frac{1}{3x（2-x）}$，
$\frac{-2x}{{x}^{2}-4}$=$\frac{-2x}{（x+2）（x-2）}$，
∴$\frac{x}{4{x}^{2}-16x+16}$，$\frac{1}{6x-3{x}^{2}}$，$\frac{-2x}{{x}^{2}-4}$的最简公分母是12x（x+2）（x-2）2，
∴$\frac{x}{4{x}^{2}-16x+16}$=$\frac{x}{4（x-2）^{2}}$=$\frac{3{x}^{2}（x+2）}{12x（x+2）（x-2）^{2}}$，
$\frac{1}{6x-3{x}^{2}}$=$\frac{1}{3x（2-x）}$=$\frac{-4（x+2）（x-2）}{12x（x+2）（x-2）^{2}}$，
$\frac{-2x}{{x}^{2}-4}$=$\frac{-2x}{（x+2）（x-2）}$=$\frac{-24{x}^{2}（x-2）}{12x（x+2）（x-2）^{2}}$．
点评 本题考查通分，解题的关键是找出几个分式的最简公分母．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
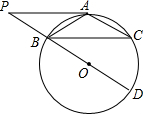如图，⊙O中，点A为$\widehat{BC}$中点，BD为直径，过A作AP∥BC交DB的延长线于点P．
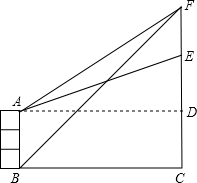如图所示，楼房AB的对面有一个建筑物EC．建筑物上方有一个信号发射塔EF．为测量EF的高度，某数学活动小组在B处测得塔尖F仰角为45°．在A处测得塔尖F仰角为α、测得点E仰角为β．已知AB高为10米，求EF的高度．（参考数据：tanα=$\frac{3}{4}$，tanβ=$\frac{9}{25}$）
