题目内容
5.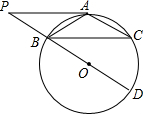 如图,⊙O中,点A为$\widehat{BC}$中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
如图,⊙O中,点A为$\widehat{BC}$中点,BD为直径,过A作AP∥BC交DB的延长线于点P.(1)求证:PA是⊙O的切线;
(2)若$BC=4\sqrt{5}$,AB=6,求sin∠ABD的值.
分析 (1)根据垂径定理得出AO⊥BC,进而根据平行线的性质得出AP⊥AO,即可证得结论;
(2)根据垂径定理得出BE=2$\sqrt{5}$,在RT△ABE中,利用锐角三角函数关系得出sin∠BAO=$\frac{\sqrt{5}}{3}$,再根据等腰三角形的性质得出∠ABD=∠BAO,即可求得求sin∠ABD=sin∠BAO=$\frac{\sqrt{5}}{3}$.
解答 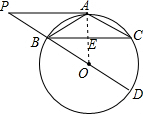 (1)证明:连结AO,交BC于点E.
(1)证明:连结AO,交BC于点E.
∵点A是$\widehat{BC}$的中点
∴AO⊥BC,
又∵AP∥BC,
∴AP⊥AO,
∴AP是⊙O的切线;
(2)解:∵AO⊥BC,$BC=4\sqrt{5}$,
∴$BE=\frac{1}{2}BC=2\sqrt{5}$,
又∵AB=6
∴$sin∠BAO=\frac{BE}{AB}=\frac{{\sqrt{5}}}{3}$,
∵OA=OB
∴∠ABD=∠BAO,
∴$sin∠ABD=sin∠BAO=\frac{{\sqrt{5}}}{3}$.
点评 此题主要考查了切线的判定,垂径定理的应用,等腰三角形的性质以及锐角三角函数关系,正确转化角度得出$sin∠ABD=sin∠BAO=\frac{{\sqrt{5}}}{3}$是解题关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
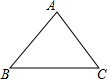 如图,已知△ABC是一个水平放置圆锥的主视图,AB=AC=5cm,$cos∠ACB=\frac{3}{5}$,则圆锥的侧面积为15πcm2.
如图,已知△ABC是一个水平放置圆锥的主视图,AB=AC=5cm,$cos∠ACB=\frac{3}{5}$,则圆锥的侧面积为15πcm2.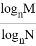 (a>0,a≠1,N>0,N≠1,M>0).例如:log223=3,log25=
(a>0,a≠1,N>0,N≠1,M>0).例如:log223=3,log25=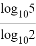 ,则log1001000=_____.
,则log1001000=_____.