题目内容

如图，在△ABC中，DE∥BC，DE分别与AB、AC相交于点D、E，若EC=2，AC=8，则DE：BC的值为（　　）
A、
2
3
B、
1
2
C、
3
4
D、
1
3
考点：相似三角形的判定与性质
专题：
分析：由DE∥BC，可得△ADE∽△ABC，然后由相似三角形的对应边成比例，即可求得DE：BC的值．
解答：解：∵DE∥BC，
∴△ADE∽△ABC，
∴DE：BC=AE：AC，
∵EC=2，AC=8，
∴AE=AB-EC=6，
∴AE：AC=6：8=3：4，
∴DE：BC=3：4．
故选C．
点评：此题考查了相似三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
三角形的面积是4cm2，底边上的高y（cm）与底边x（cm）之间的函数关系大致为（　　）
A、
B、
C、
D、
下列计算结果正确的是（　　）
A、
-b
2a2
•
a
-b2
=-
1
2ab
B、
a-b
-a+b
=-
a-b
a+b
C、
m
x
÷
n
x
=
n
m
D、(
3xy
5a
)2÷9xy=
xy
25a2
下列从左边到右边的变形，属于因式分解的是（　　）
A、（x+1）（x-1）=x2-1
B、x2-2x+1=x（x-2）+1
C、x2-4y2=（x+4y）（x-4y）
D、x2-6x+9=（x-3）2
如图，A、B的坐标分别为（0，-1），（-2，0）．若将线段AB平移至A1B1，则a+b的值为（　　）
A、2B、3C、4D、5
若0＜a＜1，a+
1
a
=6，则代数式
a
-
1
a
的值为（　　）
A、±2B、-2C、±4D、4
下列各图中，不为轴对称图形的是（　　）
A、
B、
C、
D、
如图，已知一次函数y=-3x-3的图象分别与坐标轴相交于A、C两点，且OB=OC，抛物线y=ax2+bx+c（a≠0）经过A、B、C三点，连接BC．
（1）求抛物线的解析式；
（2）若点D是线段BC下方的抛物线上一个动点，连接CD、BD，则△DBC是否有最大面积？若有，求出△DBC的最大面积和此时D点的坐标；若没有，请说明理由．
（3）若P是y轴上的动点，Q是抛物线上的动点，请直接写出以点P、Q、A、B为顶点构成平行四边形的点Q的坐标．
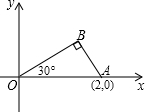如图，已知O为坐标原点，∠AOB=30°，∠ABO=90°．且点A的坐标为（2，0）．
（1）求点B的坐标；
（2）若二次函数y=ax2+bx+c的图象经过A、B、O三点，求此二次函数的关系式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网