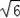题目内容
先化简：
÷（
﹣
），再从﹣2＜x＜3的范围内选取一个你最喜欢的值代入，求值．
【考点】分式的化简求值．
【专题】计算题．
【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．
【解答】解：原式=
÷
=•
=
，
当x=2时，原式=4．
【点评】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
C．400﹣64 D．4002﹣642某商场同时购进甲、乙两种商品共200件，其进价和售价如下表，
| 商品名称 | 甲 | 乙 |
| 进价（元/件） | 80 | 100 |
| 售价（元/件） | 160 | 240 |
设其中甲种商品购进x件
（1）若该商场购进这200件商品恰好用去17900元，求购进甲、乙两种商品各多少件？
（2）若设该商场售完这200件商品的总利润为y元．
①求y与x的函数关系式；
②该商品计划最多投入18000元用于购买这两种商品，则至少要购进多少件甲商品？若售完这些商品，则商场可获得的最大利润是多少元？
（3）实际进货时，生产厂家对甲种商品的出厂价下调a元（50＜a＜70）出售，且限定商场最多购进120件，若商场保持同种商品的售价不变，请你根据以上信息及（2）中的条件，设计出使该商场获得最大利润的进货方案．
B．
B．2
