题目内容
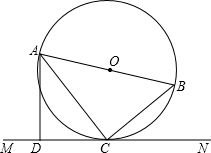 如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC,CD=6,cos∠ACD=
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC,CD=6,cos∠ACD=| 3 |
| 5 |
| A、6.5 | B、6.25 |
| C、12.5 | D、12.25 |
考点:圆周角定理,解直角三角形
专题:
分析:连接OC,先求出AD、AB的长,得出△ADC∽△ACB,根据相似三角形的性质得出比例式,进而可得出结论.
解答: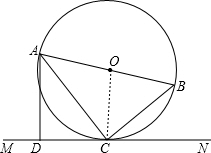 解:连接OC,
解:连接OC,
∵CD=6,cos∠ACD=
=
,
∴AC=10,
∴AD=8.
∵AB是⊙O直径,AD⊥MN,
∴∠ACB=∠ADC=90°,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴
=
,
∴
=
,
∴AB=12.5,
∴⊙O半径是
×12.5=6.25.
故选B.
 解:连接OC,
解:连接OC,∵CD=6,cos∠ACD=
| DC |
| AC |
| 3 |
| 5 |
∴AC=10,
∴AD=8.
∵AB是⊙O直径,AD⊥MN,
∴∠ACB=∠ADC=90°,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴
| AD |
| AC |
| AC |
| AB |
∴
| 8 |
| 10 |
| 10 |
| AB |
∴AB=12.5,
∴⊙O半径是
| 1 |
| 2 |
故选B.
点评:本题考查的是圆周角定理,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
按如图所示的程序计算,若开始输入n的值为1,则最后输出的结果是( )


| A、3 | B、15 | C、42 | D、63 |
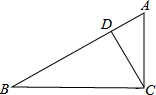 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )
如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在平面直角坐标系中,直线y=4x、y=x分别与双曲线y=
如图,在平面直角坐标系中,直线y=4x、y=x分别与双曲线y= 如图,在3×3的方格纸中,每个小方格都是边长为1的正方形,O,A,B是格点,求
如图,在3×3的方格纸中,每个小方格都是边长为1的正方形,O,A,B是格点,求
 如图,分别以正方形四边中点为圆心作四段圆弧(在正方形内相交),剪去黑色部分,就可得到一朵窗花,已知正方形的边长为10,求一朵窗花的面积.
如图,分别以正方形四边中点为圆心作四段圆弧(在正方形内相交),剪去黑色部分,就可得到一朵窗花,已知正方形的边长为10,求一朵窗花的面积. 如图,∠AOB等于∠COD,请判断∠AOC和∠BOD的大小关系并说明理由.
如图,∠AOB等于∠COD,请判断∠AOC和∠BOD的大小关系并说明理由. 如图,∠AOB=90°,直线CD将∠AOB分成2:3两部分,∠AOC大于∠BOC,那么∠BOC=
如图,∠AOB=90°,直线CD将∠AOB分成2:3两部分,∠AOC大于∠BOC,那么∠BOC=