题目内容
1.一只蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记为“+”,向负半轴运动记为“-”,从开始到结束爬行的各段路程(单位:cm)依次为+7,-5,-10,-8,+9,-6,+12,+4.(1)若A点在数轴上表示的数为-2,则蜗牛停在数轴上何处,请通过计算加以说明.
(2)若蜗牛的爬行速度为每秒$\frac{1}{2}$cm,请问蜗牛一共爬行了多少秒?
分析 (1)首先根据题意列出算式,然后进行计算,根据计算结果即可做出判断;
(2)先求得总路程,然后用路程÷速度即可求得爬行的时间.
解答 解:(1)-2+7+(-5)+(-10)+(-8)+9+(-6)+12+4=1,
所以蜗牛停在数轴上表示1的位置;
(2)|7|+|-5|+|-10|+|-8|+|9|+|-6|+|12|+|4|=61.
61÷$\frac{1}{2}$=122秒.
点评 本题主要考查的是有理数的加减,根据题意列出算式是解题的关键.

练习册系列答案
相关题目
10.某城市2013年底有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,要求到2015年底增加到363公顷.设绿化面积平均每年的增长率为x,由题意列方程正确的是( )
| A. | 300(1+x)=363 | B. | 300(1+x)2=363 | C. | 300(1+2x)=363 | D. | 363(1-x)2=300 |
11.在0,-2,1,6这四个数中,最大的数是( )
| A. | 6 | B. | 1 | C. | -2 | D. | 0 |
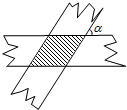 如图:两张宽度都为1cm的纸条交叉重叠在一起,两张纸条交叉的夹角为α(见图中的标注),则重叠(阴影)部分的面积表示为$\frac{1}{sinα}$.
如图:两张宽度都为1cm的纸条交叉重叠在一起,两张纸条交叉的夹角为α(见图中的标注),则重叠(阴影)部分的面积表示为$\frac{1}{sinα}$.