题目内容
4.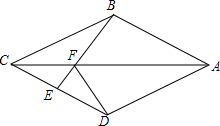 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形.
分析 (1)要证明∠BAC=∠DAC,只需证明利用SSS证明△ABC≌△ADC即可;要证明∠AFD=∠CFE先证明△ABF≌△ADF得到∠AFD=∠AFB,再结合∠AFB=∠AFD
即可得到结论;
(2)要证明四边形ABCD是菱形需要证明四条边相等,证明出∠CAD=∠ACD,即可得到AD=CD,结合题干条件即可得到结论.
解答 (1)证明:在△ABC和△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{BC=DC}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
在△ABF和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAF=∠DAF}\\{AF=AF}\end{array}\right.$,
∴△ABF≌△ADF,
∴∠AFD=∠AFB,
∵∠AFB=∠AFD,
∴∠AFD=∠CFE;
(2)证明:∵AB∥CD,
∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形.
点评 本题主要考查了菱形的判定与全等三角形的判定与性质的知识,解答(1)问的关键是利用全等三角形的性质求出∠AFD=∠AFB,解答(2)问的关键是掌握四边相等的四边形是菱形,此题难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.假定鸡蛋孵化后,鸡雏为雌或雄的羝概率相同,如果两个鸡蛋全部成功孵化,则两只鸡雏均为雄鸡的槪率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
14.如果两圆的半径分别为2cm和5cm,圆心距为6cm,那么这两个圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
 如图,Rt△ABC中,∠B=90°,BC=12,tanC=$\frac{3}{4}$.如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且$\frac{{A{P_0}}}{AB}=\frac{{A{P_1}}}{AC}$;第二步从P1跳到BC边的P2(第2次落点)处,且$\frac{{C{P_1}}}{AC}=\frac{{C{P_2}}}{BC}$;第三步从P2跳到AB边的P3(第3次落点)处,且$\frac{{B{P_2}}}{BC}=\frac{{B{P_3}}}{AB}$;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为( )
如图,Rt△ABC中,∠B=90°,BC=12,tanC=$\frac{3}{4}$.如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且$\frac{{A{P_0}}}{AB}=\frac{{A{P_1}}}{AC}$;第二步从P1跳到BC边的P2(第2次落点)处,且$\frac{{C{P_1}}}{AC}=\frac{{C{P_2}}}{BC}$;第三步从P2跳到AB边的P3(第3次落点)处,且$\frac{{B{P_2}}}{BC}=\frac{{B{P_3}}}{AB}$;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为( ) 如图,在等腰△ABC中,∠ABC=90°,D为AC边的中点,过D作DE⊥DF,交AB于E,交BC于F,BC=7,CF=3,求EF的长.
如图,在等腰△ABC中,∠ABC=90°,D为AC边的中点,过D作DE⊥DF,交AB于E,交BC于F,BC=7,CF=3,求EF的长.