题目内容
在一个布袋中放有2个红球和1个白球，它们除颜色外其它均相同充分摇匀后，先拿出1个球再放回，再拿出1个球，则两个球是同色的概率为 ．
考点：列表法与树状图法
专题：计算题
分析：先化出树状图展示所有9种等可能的结果数，再找出两个球是同色所占的结果数，然后根据概率公式求解．
解答：解：画树状图为：
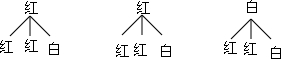
共有9种等可能的结果数，其中两次都是白球的占1种，两次都是红球的占4种，
所以两个球是同色的概率=
．
故答案为
．
共有9种等可能的结果数，其中两次都是白球的占1种，两次都是红球的占4种，
所以两个球是同色的概率=
| 5 |
| 9 |
故答案为
| 5 |
| 9 |
点评：本题考查了列表法与树状图法：利用列表法或树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求解．
练习册系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
△ABC的顶点A的坐标为（-2，4），先将△ABC沿x轴对折，再向左平移两个单位，此时A点的坐标为（ ）
| A、（2，-4） |
| B、（0，-4） |
| C、（-4，-4） |
| D、（0，4） |
如图，将平行四边形ABCD的边延长线到点E，使CE=DC，连接AE，交BC于点F．若抛物线y=ax2-2x+3的顶点坐标为（2，-3），则该抛物线有（ ）
| A、最大值-3 | B、最小值-3 |
| C、最大值2 | D、最小值2 |
点（-4，-2）关于y轴对称的点的坐标是（ ）
| A、（4，2） |
| B、（-4，2） |
| C、（-4，-2） |
| D、（4，-2） |
如图，在Rt△ABC中，∠C=90°，∠B=2∠A，BC=5，则AB=