题目内容
9. 如图,点B在射线AE上,∠1=∠2,∠3=∠4.求证:AC=AD.
如图,点B在射线AE上,∠1=∠2,∠3=∠4.求证:AC=AD.
分析 根据AAS证明△ACF≌△BDE可得结论.
解答 证明:∵∠1=∠2,∠3=∠4,
又∵∠C=∠3-∠1,∠D=∠4-∠2,
∴∠C=∠D,
在△ACB和△ADB中,
∵$\left\{\begin{array}{l}{∠1=∠2}\\{∠C=∠D}\\{AB=AB}\end{array}\right.$,
∴△ACF≌△BDE(AAS),
∴AC=AD.
点评 本题考查了全等三角形的性质和判定,在应用全等三角形的判定时,要注意三角形间的公共边和公共角,本题应用了两三角形公共边的关系.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
4.在平面直角坐标系中,点(-4,4)所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在5×4的方格纸中,每个小正方形边长为1,点O、A、B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有个3个.
如图,在5×4的方格纸中,每个小正方形边长为1,点O、A、B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有个3个.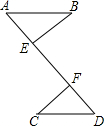 如图所示,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定 Rt△ABE≌Rt△DCF的是①②③(填入序号)
如图所示,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定 Rt△ABE≌Rt△DCF的是①②③(填入序号)