题目内容
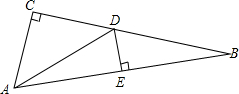 如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,且∠CAD:∠CAB=1:3,求∠B的度数.
如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,且∠CAD:∠CAB=1:3,求∠B的度数.考点:线段垂直平分线的性质
专题:
分析:设∠CAD=x,则∠CAB=3x,∠BAD=2x,再根据AB的中垂线DE交BC于点D得出AD=BD,故∠B=∠BAD=2x,由直角三角形的性质求出x的值,进而可得出结论.
解答:解:∵∠CAD:∠CAB=1:3,
∴设∠CAD=x,则∠CAB=3x,∠BAD=2x,
∵DE是AB的垂直平分线,
∴AD=BD,
∴∠B=∠BAD=2x,
∵∠C=90°,
∴∠B+∠CAB=90°,即2x+3x=90°,解得x=18°,
∴∠B=2x=36°.
∴设∠CAD=x,则∠CAB=3x,∠BAD=2x,
∵DE是AB的垂直平分线,
∴AD=BD,
∴∠B=∠BAD=2x,
∵∠C=90°,
∴∠B+∠CAB=90°,即2x+3x=90°,解得x=18°,
∴∠B=2x=36°.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
在一定条件下,若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+t,则当物体经过的路程是88米时,该物体所经过的时间为( )
| A、2秒 | B、4秒 | C、6秒 | D、8秒 |
抛物线y=-2x2-4x+1的顶点坐标是( )
| A、(1,3) |
| B、(1,-3) |
| C、(-1,-3) |
| D、(-1,3) |
 已知AD是△ABC的中线,BE是△ABD的中线,若△ABC的面积为18,则△ABE的面积为( )
已知AD是△ABC的中线,BE是△ABD的中线,若△ABC的面积为18,则△ABE的面积为( )| A、5 | B、4.5 | C、4 | D、9 |
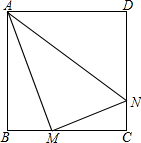 如图,正方形ABCD边长为4cm,M、N分别为BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
如图,正方形ABCD边长为4cm,M、N分别为BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直. 在梯形ABCD中,AD∥BC,AB⊥BC,AC⊥BD,AC交BD于点O,AD=1,BC=4,求
在梯形ABCD中,AD∥BC,AB⊥BC,AC⊥BD,AC交BD于点O,AD=1,BC=4,求