题目内容
(1)如图①,线段AB、CD交于点O,OA=OD、OB=OC、∠AOD=∠BOC=90°,取一点P,使得PB=PD,PA=PC,试猜想,∠DPA+∠BPC的度数;
(2)如图②,若∠AOD=α°,其他条件不变,猜想∠DPA+∠BPC的度数,并证明此结论.

(2)如图②,若∠AOD=α°,其他条件不变,猜想∠DPA+∠BPC的度数,并证明此结论.

考点:全等三角形的判定与性质
专题:
分析:(1)易证△ABP≌△CDP,可得∠PBA=∠PDC和∠PAB=∠PCD,根据三角形内角和为180°即可求得∠DPA+∠BPC=∠AOD+∠BOC,即可解题;
(2)易证△ABP≌△CDP,可得∠PBA=∠PDC和∠PAB=∠PCD,根据三角形内角和为180°即可求得∠DPA+∠BPC=∠AOD+∠BOC,即可解题.
(2)易证△ABP≌△CDP,可得∠PBA=∠PDC和∠PAB=∠PCD,根据三角形内角和为180°即可求得∠DPA+∠BPC=∠AOD+∠BOC,即可解题.
解答:解:(1)∵OA=OD、OB=OC,
∴AB=CD,
∵在△ABP和△CDP中,
,
∴△ABP≌△CDP,(SSS)
∴∠PBA=∠PDC,∠PAB=∠PCD,
∵∠DPA+∠BPC=(180°-∠PBC-∠PCB)+(180°-∠PAD-∠PDA)
=360°-(∠OBC-∠OBP)-(∠OCB-∠PCB)-(∠ODA+∠PDO)-(∠OAD+∠PAO)
=360°-∠OBC-∠OCB-∠OAD-∠ODA
=∠AOD+∠BOC,
∵∠AOD=∠BOC=90°,
∴∠DPA+∠BPC=180°;
(2)∵OA=OD、OB=OC,
∴AB=CD,
∵在△ABP和△CDP中,
,
∴△ABP≌△CDP,(SSS)
∴∠PBA=∠PDC,∠PAB=∠PCD,
∵∠DPA+∠BPC=(180°-∠PBC-∠PCB)+(180°-∠PAD-∠PDA)
=360°-(∠OBC-∠OBP)-(∠OCB-∠PCB)-(∠ODA+∠PDO)-(∠OAD+∠PAO)
=360°-∠OBC-∠OCB-∠OAD-∠ODA
=∠AOD+∠BOC,
∵∠AOD=∠BOC=α,
∴∠DPA+∠BPC=2α.
∴AB=CD,
∵在△ABP和△CDP中,
|
∴△ABP≌△CDP,(SSS)
∴∠PBA=∠PDC,∠PAB=∠PCD,
∵∠DPA+∠BPC=(180°-∠PBC-∠PCB)+(180°-∠PAD-∠PDA)
=360°-(∠OBC-∠OBP)-(∠OCB-∠PCB)-(∠ODA+∠PDO)-(∠OAD+∠PAO)
=360°-∠OBC-∠OCB-∠OAD-∠ODA
=∠AOD+∠BOC,
∵∠AOD=∠BOC=90°,
∴∠DPA+∠BPC=180°;
(2)∵OA=OD、OB=OC,
∴AB=CD,
∵在△ABP和△CDP中,
|
∴△ABP≌△CDP,(SSS)
∴∠PBA=∠PDC,∠PAB=∠PCD,
∵∠DPA+∠BPC=(180°-∠PBC-∠PCB)+(180°-∠PAD-∠PDA)
=360°-(∠OBC-∠OBP)-(∠OCB-∠PCB)-(∠ODA+∠PDO)-(∠OAD+∠PAO)
=360°-∠OBC-∠OCB-∠OAD-∠ODA
=∠AOD+∠BOC,
∵∠AOD=∠BOC=α,
∴∠DPA+∠BPC=2α.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABP≌△CDP是解题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
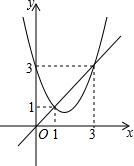 函数y1=ax2+bx+c与y2=x的图象如图所示,当y1<y2时,自变量x的取值范围是( )
函数y1=ax2+bx+c与y2=x的图象如图所示,当y1<y2时,自变量x的取值范围是( )| A、1<x<3 | B、x<1 |
| C、x>3 | D、x<1或x>3 |
 角的和、差:如图,∠AOC是∠AOB与∠BOC的和,记作
角的和、差:如图,∠AOC是∠AOB与∠BOC的和,记作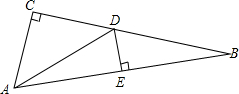 如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,且∠CAD:∠CAB=1:3,求∠B的度数.
如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,且∠CAD:∠CAB=1:3,求∠B的度数. 反比例函数y=
反比例函数y=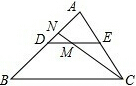 如图,在△ABC中,DE∥BC,M为DE中点,CM的延长线交AB于N,若AD:AB=2:3,求ND:BD.
如图,在△ABC中,DE∥BC,M为DE中点,CM的延长线交AB于N,若AD:AB=2:3,求ND:BD.