题目内容
有三块草地,面积分别为3
公顷,10公顷和24公顷,草地上的草一样厚,而且长得一样快,如果第一块草地饲养12头牛,可以维持4周,第二块草地饲养21头牛,可以维持9周,第三块草地饲养多少头牛可以维持18周?
| 1 |
| 3 |
考点:二元一次方程组的应用,一元一次方程的应用
专题:
分析:首先设每公顷中,初始草量为x,每周增长草量为y,进而利用第一块草地饲养12头牛,可以维持4周,第二块草地饲养21头牛,可以维持9周,得出等式求出即可,进而得出答案.
解答:解:因为“草长得一样厚一样快”所以得:
设每公顷中,初始草量为x,每周增长草量为y
且每头牛每周吃草量为a,则:
解得:
那么设第三个牧场有z头牛,所以
24(x+18y)=z×18×a
将x,y 代入得:
24(10.8a+16.2a)=18az
消去a,得:z=36.
答:第三块草地饲养36头牛可以维持18周.
设每公顷中,初始草量为x,每周增长草量为y
且每头牛每周吃草量为a,则:
|
解得:
|
那么设第三个牧场有z头牛,所以
24(x+18y)=z×18×a
将x,y 代入得:
24(10.8a+16.2a)=18az
消去a,得:z=36.
答:第三块草地饲养36头牛可以维持18周.
点评:此题主要考查了二元一次方程组的应用以及一元一次方程的应用,得出初始草量以及每周增长草量是解题关键.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
下列运算正确的是( )
| A、x2•x3=x5 |
| B、x2+x2=2x4 |
| C、(-2x2)4=16x6 |
| D、(x+3y)(x-3y)=x2-3y2 |
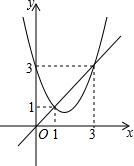 函数y1=ax2+bx+c与y2=x的图象如图所示,当y1<y2时,自变量x的取值范围是( )
函数y1=ax2+bx+c与y2=x的图象如图所示,当y1<y2时,自变量x的取值范围是( )| A、1<x<3 | B、x<1 |
| C、x>3 | D、x<1或x>3 |
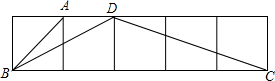 如图所示,点A、B、C、D在正方形网格的格点上,求∠BDC的度数.
如图所示,点A、B、C、D在正方形网格的格点上,求∠BDC的度数.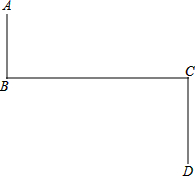 如图,AB⊥BC,CD⊥BC,AB=2,CD=3,BC=7,在BC上求一点M,当BM等于多少时,△ABM∽△CDM?
如图,AB⊥BC,CD⊥BC,AB=2,CD=3,BC=7,在BC上求一点M,当BM等于多少时,△ABM∽△CDM?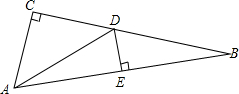 如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,且∠CAD:∠CAB=1:3,求∠B的度数.
如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,且∠CAD:∠CAB=1:3,求∠B的度数.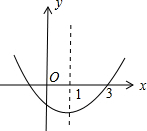 如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,且图象经过点(3,0),下列结论中,正确的是
如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,且图象经过点(3,0),下列结论中,正确的是