题目内容
如图:∠EAF=15°,AB=BC=CD=DE=EF,则∠DEF等于( ).

A、90° B、75° C、70° D、60°
D.
【解析】
试题分析:解答:【解析】
∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴∠BCD=180°-(∠CBD+∠BDC)=180°-60°=120°,
∴∠ECD=∠CED=180°-∠BCD-∠BCA=180°-120°-15°=45°,
∴∠CDE=180°-(∠ECD+∠CED)=180°-90°=90°,
∴∠EDF=∠EFD=180°-∠CDE-∠BDC=180°-90°-30°=60°,
∴∠DEF=180°-(∠EDF+∠EFC)=180°-120°=60°.
故选D.
考点:1.等腰三角形的性质;2.三角形内角和定理;3.三角形的外角性质.

练习册系列答案
相关题目



 ,0).将矩形OABC绕原点顺时针旋转90°,得到矩形
,0).将矩形OABC绕原点顺时针旋转90°,得到矩形 .设直线
.设直线 与
与 轴交于点M、与
轴交于点M、与 轴交于点N,抛物线
轴交于点N,抛物线 的图象经过点C、M、N.解答下列问题:
的图象经过点C、M、N.解答下列问题:
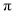 的近似值取3)
的近似值取3)
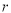 的取值范围;
的取值范围;
