题目内容
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注: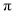 的近似值取3)
的近似值取3)
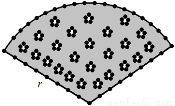
(1)求出S与r的函数关系式,并写出自变量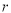 的取值范围;
的取值范围;
(2)当半径r为何值时,扇形花坛的面积最大,并求面积的最大值.
(1)S=-r2+10r.其中4<r<10.(2)5,25.
【解析】
试题分析:(1)设扇形的弧长为l米.利用已知条件可求出l和r的关系,再根据扇形的面积公式计算即可得到S与r的函数关系式;
(2)由(1)可知s和r为二次函数关系式,利用二次函数的性质求最值即可.
试题解析:(1)设扇形的弧长为l米.
由题意可知,l+2r=20.
∴l=20-2r.
∴S= (20-2r)r=-r2+10r.其中4<r<10.
(20-2r)r=-r2+10r.其中4<r<10.
(2)∵S=-r2+10r=-(r-5)2+25.
∴当r=5时,S最大值=25.
考点:1.二次函数的应用;2.弧长的计算;3.扇形面积的计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 (m为常数).
(m为常数).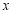 ≤2时,求函数
≤2时,求函数 的最小值(用含m的代数式表示).
的最小值(用含m的代数式表示).
 (m是常数)与直线
(m是常数)与直线 有两个交点,且这两个交点分别在抛物线对称轴的两侧,则
有两个交点,且这两个交点分别在抛物线对称轴的两侧,则 的取值范围是( )
的取值范围是( )  B.
B. C.
C. D.
D.

