题目内容
在四边形ABCD中,点M、N分别在AB、BC上,且MN=AM+CN,
(1)如图1,若四边形ABCD为正方形,通过测量、推理、猜想:∠MDN= °;
(2)如图2,若AB∥CD,AD=DC,∠A=∠B,探究:∠MDN与∠ADC之间有怎样的数量关系?请说明理由: ;
(3)如图3,若AB与CD不平行,AD=DC,要使得(2)中的结论仍然成立,∠A与∠C之间应满足什么条件?(直接回答,不需证明)
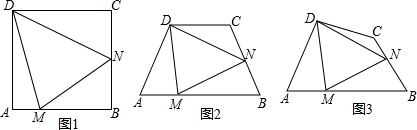
(1)如图1,若四边形ABCD为正方形,通过测量、推理、猜想:∠MDN=
(2)如图2,若AB∥CD,AD=DC,∠A=∠B,探究:∠MDN与∠ADC之间有怎样的数量关系?请说明理由:
(3)如图3,若AB与CD不平行,AD=DC,要使得(2)中的结论仍然成立,∠A与∠C之间应满足什么条件?(直接回答,不需证明)

考点:四边形综合题
专题:
分析:(1)延长BC至G使CG=AM,连接DG,利用△DAM≌△DCG得出DM=DG,再次利用△DMN≌△DGN得出∠MDN=∠GDN,运用∠MDN=
∠ADC.即可求出∠MDN的度数.
(2)延长BA至E,使AE=CN,运用△ADE≌△CDN得出DE=DN,推出△EDM≌△NDM利用角的关系得出结论.
(3)延长BC至E,使CE=AM,连接DE,在证明△DAM≌△DEC时少了一个条件,我们给它一个条件,再次运用△DMN≌△DEN得出的结论是∠MDN=
∠ADC,所以加的这个条件正是∠A与∠C应满足的条件,求出它们间的条件即可.
| 1 |
| 2 |
(2)延长BA至E,使AE=CN,运用△ADE≌△CDN得出DE=DN,推出△EDM≌△NDM利用角的关系得出结论.
(3)延长BC至E,使CE=AM,连接DE,在证明△DAM≌△DEC时少了一个条件,我们给它一个条件,再次运用△DMN≌△DEN得出的结论是∠MDN=
| 1 |
| 2 |
解答:解:(1)测量,猜想:∠MDN=45°,
证明:如图1,延长BC至G使CG=AM,连接DG,
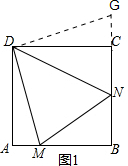
∵四边形ABCD为正方形,
∴AD=CD,∠DAB=∠DCB=∠DCG=90°
∵AM=CG,
在△DAM和△DCG中,
∴△DAM≌△DCG(SAS)
∴∠ADM=∠CDG,DM=DG,
∵MN=AM+CN,
∴MN=NG,
在△DMN和△DGN中,
,
∴△DMN≌△DGN(SSS),
∴∠MDN=∠GDN,
∴∠MDN=
∠ADC.
∴∠MDN=∠GDN=
×90°=45°
故答案为:45.
(2)∠MDN=
∠ADN,
证明:如图2,延长BA至E,使AE=CN,
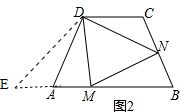
∵AB∥CD,
∴∠B+∠C=180°,
∵∠DAB=∠B,
∴∠DAB+∠C=180°,
∵∠DAE+∠DAB=180°,
∴∠DAE=∠C,
∵AD=DC,
在△ADE和△CDN中,
∴△ADE≌△CDN(SAS)
∴DE=DN,∠ADE=∠CDN,
∵MN=AM+CN,
∴MN=AM+AE=EM,
又∵DM为公共边,
在△EDM和△NDM中,
∴△EDM≌△NDM(SSS)
∴∠MDE=∠MDN,
∴∠MDN=∠CDN+∠ADM,
∴∠MDN=
∠ADC,
故答案为:∠MDN=
∠ADC.
(3)如图3,延长BC至E,使CE=AM,连接DE,
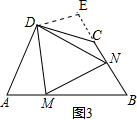
∵AD=DC,AM=CE,
现在要使△DAM≌△DEC少一个条件,假设∠A=∠ECD,
则有△DAM≌△DEC(SAS)
∴DE=DM,∠ADM=∠CDE,
∵MN=AM+CN=NE,DN为公共边,
在△DMN和△DEN中,
∴△DMN≌△DEN(SSS)
∴∠MDN=∠EDN,
∴∠MDN=
∠ADC.
结论成立只需一个条件∠A=∠ECD,即∠A+∠DCN=180°,就是原图的∠A+∠C=180°.
证明:如图1,延长BC至G使CG=AM,连接DG,

∵四边形ABCD为正方形,
∴AD=CD,∠DAB=∠DCB=∠DCG=90°
∵AM=CG,
在△DAM和△DCG中,
|
∴△DAM≌△DCG(SAS)
∴∠ADM=∠CDG,DM=DG,
∵MN=AM+CN,
∴MN=NG,
在△DMN和△DGN中,
|
∴△DMN≌△DGN(SSS),
∴∠MDN=∠GDN,
∴∠MDN=
| 1 |
| 2 |
∴∠MDN=∠GDN=
| 1 |
| 2 |
故答案为:45.
(2)∠MDN=
| 1 |
| 2 |
证明:如图2,延长BA至E,使AE=CN,

∵AB∥CD,
∴∠B+∠C=180°,
∵∠DAB=∠B,
∴∠DAB+∠C=180°,
∵∠DAE+∠DAB=180°,
∴∠DAE=∠C,
∵AD=DC,
在△ADE和△CDN中,
|
∴△ADE≌△CDN(SAS)
∴DE=DN,∠ADE=∠CDN,
∵MN=AM+CN,
∴MN=AM+AE=EM,
又∵DM为公共边,
在△EDM和△NDM中,
|
∴△EDM≌△NDM(SSS)
∴∠MDE=∠MDN,
∴∠MDN=∠CDN+∠ADM,
∴∠MDN=
| 1 |
| 2 |
故答案为:∠MDN=
| 1 |
| 2 |
(3)如图3,延长BC至E,使CE=AM,连接DE,

∵AD=DC,AM=CE,
现在要使△DAM≌△DEC少一个条件,假设∠A=∠ECD,
则有△DAM≌△DEC(SAS)
∴DE=DM,∠ADM=∠CDE,
∵MN=AM+CN=NE,DN为公共边,
在△DMN和△DEN中,
|
∴△DMN≌△DEN(SSS)
∴∠MDN=∠EDN,
∴∠MDN=
| 1 |
| 2 |
结论成立只需一个条件∠A=∠ECD,即∠A+∠DCN=180°,就是原图的∠A+∠C=180°.
点评:本题主要考查了四边形综合题,本题要正确画出辅助线,并多次运用三角形全等的判定及性质,找出全等三角形对应的角与线段是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知三角形内的一个点到它的三边距离相等,那么这个点是( )
| A、三角形的外心 |
| B、三角形的重心 |
| C、三角形的内心 |
| D、三角形的垂心 |
已知|x|=3,y2=4且x<y,则xy的值等于( )
| A、6 | B、-6 |
| C、6或-6 | D、以上答案都不对 |
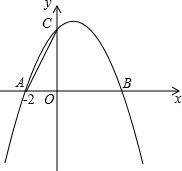 如图,已知抛物线y=ax2+bx+4与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
如图,已知抛物线y=ax2+bx+4与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线x=1. 如图,已知抛物线y=
如图,已知抛物线y= 如图,已知正比例函数y=ax与反比例函数
如图,已知正比例函数y=ax与反比例函数